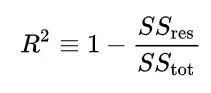When I have a linear regression and I want to determine uncertainty in the slope from the quality of the fit (ignoring any uncertainty from error bars for now), I generally use
$$ \sigma_m = m \sqrt{\frac{1/R^2 - 1}{n-2}} $$
where $R^2$ is the coefficient of determination, $n$ is the number of data points, $m$ is the slope, and $\sigma_m$ is the uncertainty in the slope.
For a set of data that is highly non-linear, and thus has a very low-quality fit, $R^2$ may become negative. However, when $R^2 \leq 0$, the argument of the square root becomes negative, and thus the uncertainties become imaginary. Is there a method for determining uncertainty due to the quality of a fit under these circumstances?