2

I am aware that it is printed at the bottom of the summary function output, but only using the other things displayed from the summary function, how would you work out the multiple R-Squared value? I know that the formula for it is:

RegressionSS/[RegressionSS+ResidualSS]

But I don't know how to find these on the summary function either.

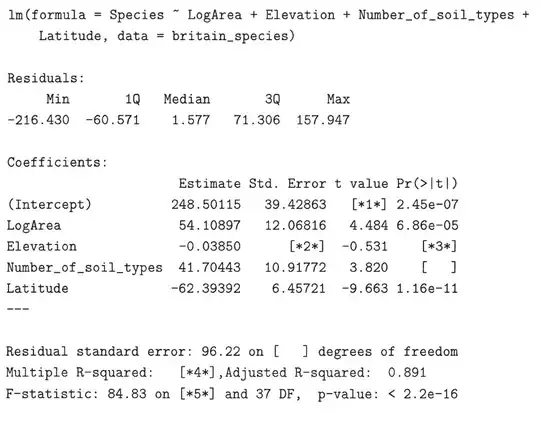
enter image description here

MrUsername12
  • 35
  • 4

1 Answers1

0

This looks like a homework problem, so I'll be a bit coy with my answer.

If you're allowed to use adjusted $R^2$, you can do it.

$$R^2_{adj} = 1 - (1-R^2)\dfrac{n-1}{n-p}$$

Here, $p$ is the number of parameters estimated in the $\beta$ vector including the intercept.

The printout gives you $R^2_{adj}$. The printout also gives you the number of parameters you've estimated ($p$) and the number of observations ($n$) used to fit the equation. Then it's just algebra.

Do you see how you get $p$ and $n$ from the printout? (That's what makes this a statistics question for Cross Validated instead of a programming question that should be on Stack Overflow.)

EDIT

After discussing in the comments and chat enough that I can see that you get how to do the problem, I will give a full solution.

The first $df$ in the F-stat is $p-1$, where $p$ is the number of parameters including the intercept. There are five parameters, do $df_1=4$. Then it is given that $df_2=37$.

$df_2 = n-p$, so $n=df_2+p = 37+5=42$.

Now we go to the $R^2_{adj}$ equation and plug in these values.

$$ R^2_{adj} = 1 - (1-R^2)\dfrac{n-1}{n-p} $$

$$ 0.891 = 1 - (1-R^2)\dfrac{41}{37} $$

The algebra shows that $R^2 = 0.9016341463414634$.

A comment by whuber mentioned that you can relate the F-stat to $R^2$, too. From this question, we see that the relationship is $F = \dfrac{ R^2 }{ 1- R^2} \times \dfrac{ df_2 }{ df_1 }$. Let's plug in the numbers.

$$ 84.83 = \dfrac{ R^2 }{ 1- R^2} \times \dfrac{ 37 }{ 4} $$

The algebra shows that $R^2 = 0.9016794217687075$. This is almost the same as the value from the other method, and if you consider only the three significant figures in the given $R^2_{adj}$ value, they are the same: $0.902$. The F-stat and $R^2_{adj}$ value are rounded in the printout, so I think it is fair to round to three decimal places and say that $R^2 = 0.902$.

Dave
  • 28,473
  • 4
  • 52
  • 104
  • This is a past exam question that I am doing as revision. I have the answer in front of me but I do not understand how they get to it, as all that is stated in the mark scheme is $R^2$ = RegrSS/(RegrSS + ResidSS) = 0.912. If I understand correct, n-p=degree of freeom where p is the amount of parameters [including the intercept?] In this case adjusted $R^2$=0.891, DF=37 and there are 4 predictor variables, and an intercept but when subbing this in, it doesn't give the answer shown in the mark scheme – MrUsername12 May 27 '20 at 20:11
  • Please edit your original post with a photo or screenshot of the original question. With so many numbers flying around, I want to make sure we both agree on what each means. – Dave May 27 '20 at 20:15
  • Done. There are other gaps which I have worked out, but I don't think any of them are relevant here. – MrUsername12 May 27 '20 at 20:17
  • Well how do the degrees of freedom of the F-stat relate to the number of parameters you estimate (you have to estimate the intercept?) and the sample size? – Dave May 27 '20 at 20:45
  • I just used degrees of freedom= n [sample size] - p [parameters], so n was 42 and p was 5. Is that wrong? – MrUsername12 May 27 '20 at 20:55
  • Are those numbers giving you the right answer or the wrong answer? – Dave May 27 '20 at 21:01
  • Wrong. It gives me 0.904 – MrUsername12 May 27 '20 at 21:08
  • I've made a correction to the post. I'm used to thinking of the intercept as being a parameter to estimate and thus contributing to $p$, and the source where I got the equation was not my one-time textbook and did not consider the intercept as contributing to $p$, hence the subtraction of $1$. – Dave May 27 '20 at 21:13
  • Why is the intercept not a parameter here then? – MrUsername12 May 27 '20 at 21:15
  • Let us [continue this discussion in chat](https://chat.stackexchange.com/rooms/108560/discussion-between-dave-and-mrusername12). – Dave May 27 '20 at 21:15