66

It is often recommended to take the square root when you have count data. (For some examples on CV, see @HarveyMotulsky's answer here, or @whuber's answer here.) On the other hand, when fitting a generalized linear model with a response variable distributed as Poisson, the log is the canonical link. This is sort of like taking a log transformation of your response data (although more accurately it is taking a log transformation of $\lambda$, the parameter that governs the response distribution). Thus, there is some tension between these two.

  • How do you reconcile this (apparent) discrepancy?
  • Why would the square root be better than the logarithm?
Community
  • 1
gung - Reinstate Monica
  • 132,789
  • 81
  • 357
  • 650

1 Answers1

55

The square root is approximately variance-stabilizing for the Poisson. There are a number of variations on the square root that improve the properties, such as adding $\frac{3}{8}$ before taking the square root, or the Freeman-Tukey ($\sqrt{X}+\sqrt{X+1}$ - though it's often adjusted for the mean as well).

In the plots below, we have a Poisson $Y$ vs a predictor $x$ (with mean of $Y$ a multiple of $x$), and then $\sqrt{Y}$ vs $\sqrt{x}$ and then $\sqrt{Y+\frac{3}{8}}$ vs $\sqrt{x}$.

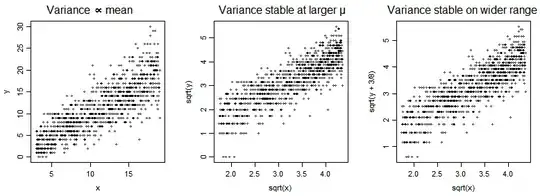
enter image description here

The square root transformation somewhat improves symmetry - though not as well as the $\frac{2}{3}$ power does [1]:

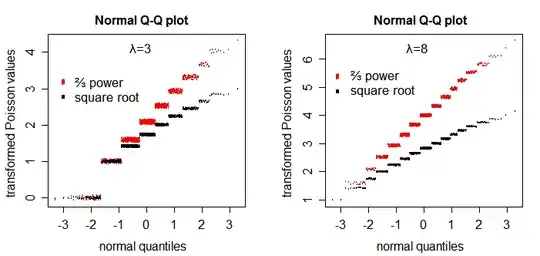
enter image description here

If you particularly want near-normality (as long as the parameter of the Poisson is not really small) and don't care about/can adjust for heteroscedasticity, try $\frac{2}{3}$ power.

The canonical link is not generally a particularly good transformation for Poisson data; log zero being a particular issue (another is heteroskedasticity; you can also get left-skewness even when you don't have 0's). If the smallest values are not too close to 0 it can be useful for linearizing the mean. It's a good 'transformation' for the conditional population mean of a Poisson in a number of contexts, but not always of Poisson data. However if you do want to transform, one common strategy is to add a constant $y^*=\log(y+c)$ which avoids the $0$ issue. In that case we should consider what constant to add. Without getting too far from the question at hand, values of $c$ between $0.4$ and $0.5$ work very well (e.g. in relation to bias in the slope estimate) across a range of $\mu$ values. I usually just use $\frac12$ since it's simple, with values around $0.43$ often doing just slightly better.

As for why people choose one transformation over another (or none) -- that's really a matter of what they're doing it to achieve.

[1]: Plots patterned after Henrik Bengtsson's plots in his handout "Generalized Linear Models and Transformed Residuals" see here (see first slide on p4). I added a little y-jitter and omitted the lines.

Glen_b
  • 257,508
  • 32
  • 553
  • 939
  • +1, thanks for your help. I gather the square root (or slight variations) is best for normalizing & stabilizing the variance of the Poisson, whereas the log is best for linearizing the mean. Your point about the problem w/ $\log 0$ is also a good one. Nonetheless, I find it counter-intuitive that the best transformation differs between these two contexts. – gung - Reinstate Monica Dec 22 '12 at 17:44
  • 1
    OK, I've been thinking about what you've put here, & here's my synthesis: The optimal transformations differ in these 2 situations b/c what you're trying to achieve differs. The sqrt is better for stabilizing the variance & normalizing the distribution. The log maps the interval $(0, +\infty)$ to $(-\infty, +\infty)$ which allows the transformation of the mean, $\lambda$, to be linear in model parameters. The sqrt does not have this property. W/ a GLiM, it doesn't matter that the variance isn't constant, b/c the response distribution is set as Poisson. Is that about right? – gung - Reinstate Monica Dec 23 '12 at 00:00
  • 2
    What will be linear in the parameters *depends on the model*. It's perfectly possible for that linearity to be on the original scale or the square root scale or some other scale. Even the - useful/important - 'maps to the real line' property isn't unique to the log function. The reason the log link is 'natural' is because of the way it simplifies the GLM by having a sufficient statistic of $X'y$. – Glen_b Dec 23 '12 at 01:57
  • 2
    +1 The square root is merely a starting point for dealing with count data. The logarithm also is a good choice. The data will often tell you which one is more successful in obtaining a useful and succinct description. Gung, in the [answer you refer to](http://stats.stackexchange.com/a/46350), the demonstration that the square root was a good choice lies in the symmetric distribution of the non-outlying residuals apparent in the right hand figure. When you vary the parameters of the simulation, you will find that symmetry is maintained. – whuber Dec 24 '12 at 16:09
  • @whuber When you say the logarithm is a good choice -- it would seem to have a problem with $\log(0)$. That requires either doing something other than $\log(X)$ (such as actually using a shifted-log) or restricting it to cases with no zeros. The first makes the good choice actually a different choice and the second seems to diminish its value rather significantly. – Glen_b Dec 25 '12 at 11:02
  • 2
    @Glen I did not say logs are *always* a good choice. But sometimes they are superior to roots. When zero counts appear then yes, you need a ["started" logarithm](http://stats.stackexchange.com/questions/6150/is-visualization-sufficient-rationale-for-transforming-data/6177#6177). Other threads here have [discussed ways to obtain a starting value](http://stats.stackexchange.com/questions/41361/choosing-c-such-that-logx-c-would-remove-skew-from-the-population/41377#41377). When there are no zero counts in the data, then there will be no problems with logs at all. – whuber Dec 26 '12 at 15:39
  • Perhaps it is worth annotating this thread with an indication that there can be limitations to transformations of count data, esp. if there are 0s that require a log(x+1). A good ref is Bolker(2012) Generalized linear models for disease ecologists, and citations therein. – N Brouwer Dec 27 '12 at 19:47
  • Hi guys, hi @whuber! Why would you transform the count data themselves? All these approaches seem a bit "dirty" - i.e. why $\sqrt{x+1}$ and not $\sqrt{x+2}$, the same for $\log{x+1}$ etc. I think the best and cleanest is the GLM approach when you **log-transform the expected value**, not the count itself! So no problem with $\text{log}(0)$. This approach is not only useful for the response variable, **[it can even be used in the predictor!](http://stats.stackexchange.com/q/61756/5509)**. – Tomas Nov 28 '13 at 20:02
  • 2
    @Tomas As for why Freeman-Tukey or $\sqrt{x+3/8}$ rather than $\sqrt{x}$ or $\sqrt{x+c}$ for some other $c$, there are good reasons for both Freeman-Tukey and $\sqrt{x+3/8}$ (for example, to do with making skewness closer to 0), but if you want to get into those in detail, that would be a whole new question. – Glen_b Nov 28 '13 at 22:02
  • @glen_b my comment above suggest exactly the opposite direction than arguing which constant is the best.. – Tomas Nov 29 '13 at 11:16
  • @Tomas That was in response to "why $\sqrt{x+1}$ and not $\sqrt{x+2}$"; the implication of your comment does have some response - the numbers aren't just arbitrary. – Glen_b Nov 29 '13 at 16:50
  • If $X$ is Poisson($\lambda$) then $Y = \sqrt{X+ 1/4}$ has approximately mean $\sqrt{\lambda}$ and variance 1/4. Moreover, for large $\lambda$, $Y$ will be Gaussian. – utobi Jun 25 '15 at 11:59
  • @utobi Yes, the $\frac14$ option should be mentioned, thanks. The approximate variance term applies for adding 0, 3/8, 1/4 or any small fraction, as does the asymptotic Gaussianity. Brown, Zhang and Zhao (2001) encourage the use of $\frac14$ because of the improved accuracy of the mean; in [Brown and Zhao](http://www-stat.wharton.upenn.edu/~lzhao/papers/MyPublication/Newtest_Sankhya_2002.pdf) (2002) they prefer $\frac38$ because of the more stable variance. Which is better depends on the application. – Glen_b Jun 25 '15 at 13:27