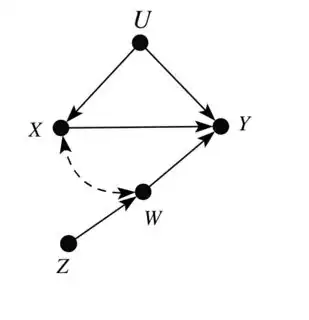
I am self-studying Causality: Models, Reasoning, and Inference, by Judea Pearl, and there is a question I am particularly stumped on. It reads like this:
Problem Statement: Given this fragment of a Bayesian Network, add two variables to the network, $Z$ and $W,$ such that the following three conditions hold simultaneously:
- $Z$ and $X$ are dependent given $W,$ and
- $Z$ and $U$ are independent given $W.$
- $Z$ and $W$ are ancestors of $Y$ but not of $X.$
My Work So Far: Because $Z$ and $W$ must be ancestors of $Y$ but not $X,$ there can be no arrows going into $X$ (from $Z$ or $W$). Because $U$ is an ancestor of $X,$ there can be no arrows going into $U,$ either. Likely, though, we will need arrows going into $Y.$ As I see it, there are essentially two possibilities: arrows going out of $U,$ or arrows going out of $X.$ As we need dependence on $X$ and not $U,$ I'm going to guess that we need arrows going out of $X.$ That means there are essentially four possibilities:
a satisfies 1 and 3, but not 2. b satisfies 2 and 3, but not 1. c satisfies 1 and 3, but not 2. And d satisfies 1 and 3, but not 2.
Do I need to look at $U?$ Or do you have other ideas?
Thanks for your time!