2

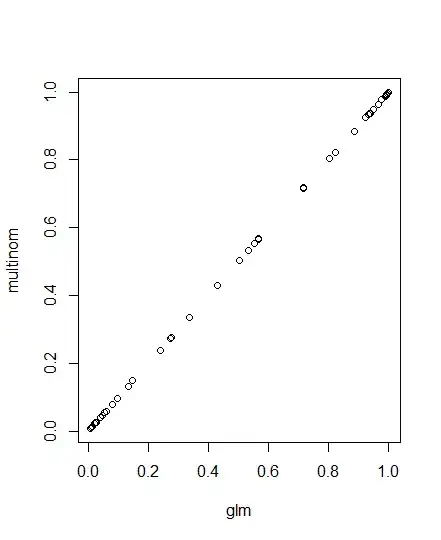
I'm trying to understand the differences I see when applying multinomial logistic regression models in R using nnet and mgcv. For comparison purposes with glm() let's take only two levels for the dependent variable. The additive model success ~ numeracy + anxiety retrieves identical results for all approaches. However for the interaction term nnet generates very different results as compared to the other two.

A <- structure(list(numeracy = c(6.6, 7.1, 7.3, 7.5, 7.9, 7.9, 8, 
8.2, 8.3, 8.3, 8.4, 8.4, 8.6, 8.7, 8.8, 8.8, 9.1, 9.1, 9.1, 9.3, 
9.5, 9.8, 10.1, 10.5, 10.6, 10.6, 10.6, 10.7, 10.8, 11, 11.1, 
11.2, 11.3, 12, 12.3, 12.4, 12.8, 12.8, 12.9, 13.4, 13.5, 13.6, 
13.8, 14.2, 14.3, 14.5, 14.6, 15, 15.1, 15.7), anxiety = c(13.8, 
14.6, 17.4, 14.9, 13.4, 13.5, 13.8, 16.6, 13.5, 15.7, 13.6, 14, 
16.1, 10.5, 16.9, 17.4, 13.9, 15.8, 16.4, 14.7, 15, 13.3, 10.9, 
12.4, 12.9, 16.6, 16.9, 15.4, 13.1, 17.3, 13.1, 14, 17.7, 10.6, 
14.7, 10.1, 11.6, 14.2, 12.1, 13.9, 11.4, 15.1, 13, 11.3, 11.4, 
10.4, 14.4, 11, 14, 13.4), success = c(0L, 0L, 0L, 1L, 0L, 1L, 
0L, 0L, 1L, 0L, 1L, 1L, 0L, 1L, 0L, 0L, 0L, 0L, 0L, 1L, 0L, 0L, 
1L, 1L, 1L, 0L, 0L, 0L, 1L, 0L, 1L, 0L, 0L, 1L, 1L, 1L, 1L, 1L, 
1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L)), .Names = c("numeracy", 
"anxiety", "success"), row.names = c(NA, -50L), class = "data.frame")

library(nnet)
library(mgcv)

model1 <- glm(success ~ numeracy * anxiety, binomial, data=A)
summary(model1)
#Coefficients:
#                 Estimate Std. Error z value Pr(>|z|)
#(Intercept)       0.87883   46.45256   0.019    0.985
#numeracy          1.94556    4.78250   0.407    0.684
#anxiety          -0.44580    3.25151  -0.137    0.891
#numeracy:anxiety -0.09581    0.33322  -0.288    0.774

model2 <- gam(list(A$success~A$numeracy*A$anxiety),family=mgcv::multinom(K=1))
summary(model2)
#Parametric coefficients:
#                     Estimate Std. Error z value Pr(>|z|)
#(Intercept)           0.87883   46.45422   0.019    0.985
#A$numeracy            1.94556    4.78272   0.407    0.684
#A$anxiety            -0.44580    3.25162  -0.137    0.891
#A$numeracy:A$anxiety -0.09581    0.33324  -0.288    0.774

model3 <- nnet::multinom(success ~ numeracy*anxiety, data = A)
summary(model3)
#Coefficients:
#                      Values  Std. Err.
#(Intercept)       0.69335106 0.07083273
#numeracy          1.96445284 0.70967242
#anxiety          -0.43283777 0.16992672
#numeracy:anxiety -0.09712809 0.04876127
z <- summary(model3)$coefficients/summary(model3)$standard.errors
p <- (1 - pnorm(abs(z), 0, 1)) * 2
p
#     (Intercept)         numeracy          anxiety numeracy:anxiety 
#     0.000000000      0.005638205      0.010859038      0.046380895
albifrons
  • 123
  • 4

1 Answers1

2

These models are not all that different - in fact, by way of their fit to the data and predictions, they're almost identical.

> data.frame(glm=AIC(model1), multinom=AIC(model3))
      glm multinom
1 36.2007 36.20072

> cor(data.frame(glm=predict(model1, type="response"), multinom=predict(model3, type="prob")))
               glm  multinom
glm      1.0000000 0.9999999
multinom 0.9999999 1.0000000

> plot(data.frame(glm=predict(model1, type="response"), multinom=predict(model3, type="prob")))

enter image description here

The issue you've run into is in regards to scaling for nnet::multinom. Specifically, the documentation for multinom states:

Details

multinom calls nnet. The variables on the rhs of the formula should be roughly scaled to [0,1] or the fit will be slow or may not converge at all.

Thus, the way multinom fit to the data is the best it could achieve given the scaling it expected is not true for data frame A. Of course, this did affect the coefficients and standard errors in non-trivial ways as the original post suggests but didn't actually impact how well it modeled the data.

The results between the functions synchronize with respect to coefficient and standard error values once the data in A are scaled as multinom expects as is illustrated below using data frame B with scale()-ed predictors.

> B <- data.frame(s_num = scale(A$numeracy), s_anx = scale(A$anxiety), succ = A$success)
> model1s <- glm(succ ~ s_num*s_anx, data = B, binomial)
> summary(model1s)

Call:
glm(formula = succ ~ s_num * s_anx, family = binomial, data = B)

Deviance Residuals: 
     Min        1Q    Median        3Q       Max  
-1.85712  -0.33055   0.02531   0.34931   2.01048  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)  
(Intercept)   1.1836     0.6639   1.783   0.0746 .
s_num         1.5143     0.6976   2.171   0.0300 *
s_anx        -3.0488     1.2484  -2.442   0.0146 *
s_num:s_anx  -0.4934     1.7159  -0.288   0.7737  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 68.029  on 49  degrees of freedom
Residual deviance: 28.201  on 46  degrees of freedom
AIC: 36.201

Number of Fisher Scoring iterations: 7

> model3s <- nnet::multinom(succ ~ s_num*s_anx, data = B)
# weights:  5 (4 variable)
initial  value 34.657359 
iter  10 value 14.100365
final  value 14.100352 
converged
> summary(model3s)
Call:
nnet::multinom(formula = succ ~ s_num * s_anx, data = B)

Coefficients:
                Values Std. Err.
(Intercept)  1.1836058 0.6639332
s_num        1.5142944 0.6976816
s_anx       -3.0487571 1.2485004
s_num:s_anx -0.4933808 1.7159948

Residual Deviance: 28.2007 
AIC: 36.2007 
> zs <- summary(model3s)$coefficients/summary(model3s)$standard.errors
> ps <- (1 - pnorm(abs(zs), 0, 1)) * 2
> ps
(Intercept)       s_num       s_anx s_num:s_anx 
 0.07463219  0.02997154  0.01460877  0.77371509
jluchman
  • 476
  • 2
  • 11