2

I am using the Lmer function from the lmerTest in R to test the significant of fixed effects [Training (2 levels factor: H/GD) & Value (2 levels factor:D/ND)] on % of responses (numeric: ResTest), with a repeated mesures design (20 subjects tested in the 4 conditions: H/D, H/ND, GD/D, GD/ND = 4 observation / subject).

Here is my model, with Subject as a random factor:

mymodel <- lmer(ResTest~Value + Training + Value:Training + (1|Subject), data = Data)

This what the summary gives me:

my model summary

Residuals are symmetrical, all fixed effects are significant.

Using the r.squaredGLMM(mymodel) I obtained the R2 for the model, which is 0.9873067.

I then run diagnostics of my model, first checking for the normality of my residuals, using qqnorm(residuals(mymodel), ylab="Residuals for mymodel") & qqline(residuals(mymodel)) . That is what I get and where problems begins: my residuals are heavy tailed.

QQ plot

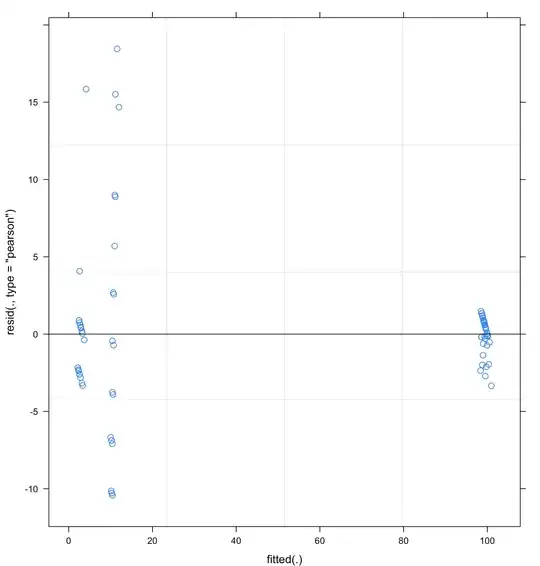
Plus, when I plot the residuals vs fitted, there is some large y axis data point and data point don't tend to cluster towards the middle of the plot at all. But I mean, my data are like this, with two of the conditions inducing almost always 100 % of responses and the 2 others inducing near 0% of responses and nothing in the middle.

residuals vs fitted

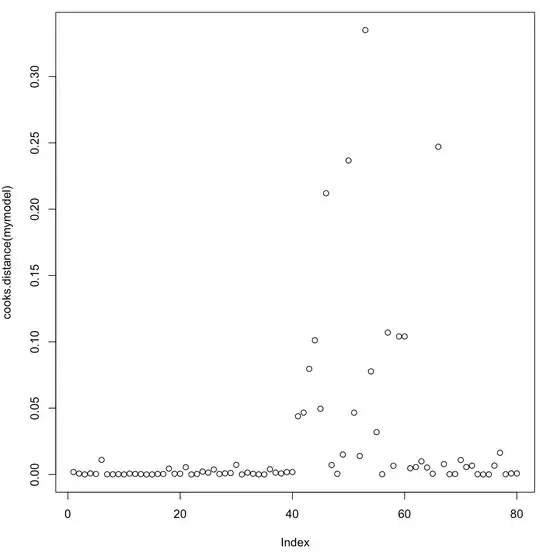
I tried to asses the impact of some of my data point with plot(cooks.distance(mymodel)) to see if there is something here, but it's seems that no data point have an excessive influence on my model.

cooks distance

With all of this, I am not sure how I can trust my model (and the very good R squared) and I really would like to improve it (and understand it). Have I gone in a completely bad direction ?

Also, is there a reason why I should use lmer instead of lme ? Because I have seen this heavy package, with the heavyLme fonction ("This function fits a linear mixed-effects model under heavy-tailed errors using the formulation described in Pinheiro et al. (2001)").

So I tried my model like this:

model <- lme(ResTest~Value + Training, random = ~1|Subject, data = Data)

and obtained same results.

I tried to do the heavyLme fonction, but it didn't work because I don't get what is this "groups" argument...

mymodelheavy <- heavyLme(ResTest~Value + Training + Value*Training ,
                         random = ~Subject, groups = ~ ?,  data = Data)

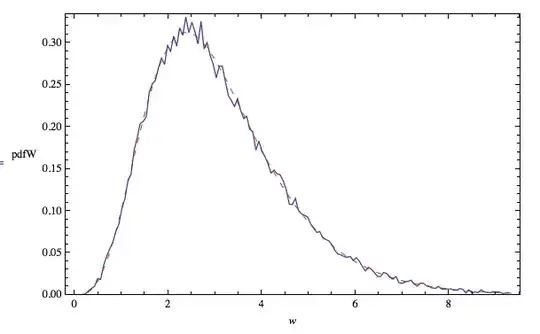
Here is the density graph of my dependent variable (% of responses), using plot(density(Data$ResTest)).

outcome density

and here is a plot density of the residuals of my lmer model (plot(density(residuals(mymodel)): 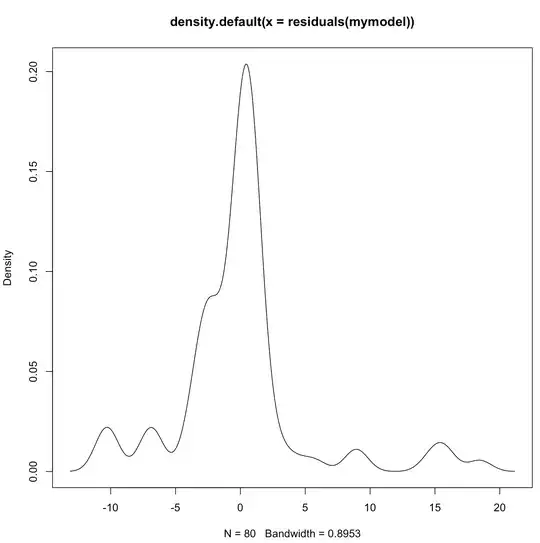residual density

I hope someone can help me with all of this.

EDIT: My data are binomial and I should not have done lmer in the first place, but glmer with family=binomial and a logit link. Works much better that way !

Emilie Durosoir
  • 23
  • 6
  • I don't trust that r-squared value at all. Can you post an image of the kernal density plot of your outcome? `plot(density(x))` You should also check out `robustlmm` and `heavy`. See https://cran.r-project.org/web/packages/robustlmm/vignettes/rlmer.pdf It goes through the different options for heavy-tailed distributions. – Erik Ruzek Apr 14 '20 at 14:50
  • I tried the heavyLme (see in the end of my post) but I don't get the groups argument, could you help on that ? I see that the robustlm package have to do with sensibility for outliers, but I don't think this is the problem here as cook distance didn't show anything ? Any way, I tried the rlmer fonction like this: `mymodel – Emilie Durosoir Apr 14 '20 at 15:34
  • That histogram says it all. You do not have a unimodal distribution. `lm` and `lmer` and their offshoots are designed to model unimodal distributions or 0/1, count, rates, etc. You have a bimodal distribution, which could could be a mixture of two normal distributions. See https://stats.stackexchange.com/questions/310064/mixture-models-vs-mixed-models for a start. – Erik Ruzek Apr 14 '20 at 16:10
  • So if I get it, what I really want would be a "mixed effect mixture mode"l... is there some formula do to that, like for lmer ? I saw some stuff like FLXMRlmer, but I don't understand a thing about it... lmer already was complicated for me :/ – Emilie Durosoir Apr 14 '20 at 17:13
  • The residuals plot density shows that the distribution is not binomial (see post), so should I still do a mixted effect mixture model? – Emilie Durosoir Apr 14 '20 at 17:25
  • The q-q plot shows that you have major issues with the residuals from a linear model. That, combined with the density plot of your outcome, suggest that you need a different approach. I do not know much about multilevel mixture models, I'm afraid. The one program I know you can estimate them in is Mplus, but that is not freeware. There is a student version you can play with that limits you to seven variables, I think. – Erik Ruzek Apr 14 '20 at 18:08

0 Answers0