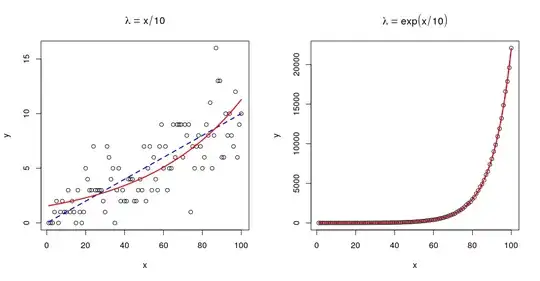
glm() of the following data gives intercept 0.56916 and slope x .018. But the true slope should be 1/10. Does anybody know why glm() can not recover the true slope? Thanks.
R> tmp = data.frame(x=seq_len(100), y=rpois(100, lambda=seq_len(100)/10))
R> fit = glm(y ~ x, family=poisson, data=tmp)
R> fit
Call: glm(formula = y ~ x, family = poisson, data = tmp)
Coefficients:
(Intercept) x
0.56916 0.01812
Degrees of Freedom: 99 Total (i.e. Null); 98 Residual
Null Deviance: 252.6
Residual Deviance: 125.1 AIC: 442.3
R> library(ggplot2)
R> p=qplot(tmp$x, predict(fit))
R> ggsave(p, file='/tmp/glm_poisson_fit.png')
Saving 7 x 7 in image
R>