0

I have two sigmoid functions, sig1 and sig2, made with this function sigmoid = function(x, A =1, mu=0, ss = 1) A*1 / (1 + exp(-(x-mu) * ss)). Since they have a true offset of 10 (mu1=50 and mu2=60) I expected their cross-correlation function to peak at a lag of 10. My non-mathematical intuition is that cross-correlation "slides" one of the curves over by a given lag, correlates, and repeats for multiple lags. When I do this by myself in code (my.ccf in the code below) I do directly recover the lags I designed into the curves. However, ccf, the real R cross-correlation function, returns max lag of 4 (see below). What's going on?

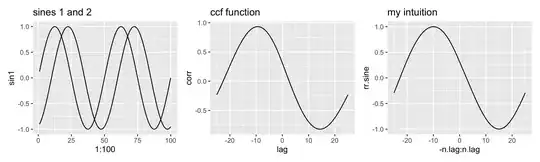
enter image description here

To replicate, I did the same thing for two sines. They have a designed "lag" of 10 (see below). Here, the max lag returned by ccf (9) is closer to the designed-in value, but isn't exactly equal. My intuitive function returns 10, the "correct" answer.

enter image description here

Why doesn't the max of the two cross-correlation functions (4 and 9) exactly equal the lag I coded into the curves (10 and 10, respectively)? What's wrong with my intuition? Edit: As pointed out by Whuber, why isn't the max of ccf 1, since these are identical and perfectly aligned vectors.

(code)

# sigmoid function
sigmoid = function(x, A =1, mu=0, ss = 1)  A*1 / (1 + exp(-(x-mu) * ss))

# my intuition
my.ccf = function(x,y, lag=20) {
  lags = -lag : lag

  # add padding to y
  y.padded = c(rep(NA,lag), y, rep(NA,lag))

  # correlate
  rr = numeric(length(lags))
  for (ii in 1:length(lags)) {
    # apply lag to y.padded
    I = (1:length(x)) + (ii-1)
    y.lagged = y.padded[I]

    rr[ii] = cor.test(x, y.lagged)$estimate
  }
  return(rr)
}

# make sigmoids and cross-correlate
sig1 = sigmoid(1:100, mu=50, ss=1/3)
sig2 = sigmoid(1:100, mu=60, ss=1/3)
ccf.sig=ccf(sig1, sig2, plot=F)
rr.sig = my.ccf(sig2,sig1,lag=16)

# do the same with sines
sin1 = sin((1:100) * 4*pi/100)
sin2 = sin(((1:100) - 10) * 4*pi/100)
ccf.sine=ccf(sin1, sin2,plot=F)
rr.sine = my.ccf(sin2,sin1,lag=16)

# plot sigmoids + ccf.sig
p1 = ggplot() + geom_line( aes(x=1:100,y=sig1)) + 
  geom_line(aes(x=1:100,y=sig2)) + ggtitle("sigmoids 1 and 2")
p2 = ggplot(data.frame(lag=ccf.sig$lag, corr=ccf.sig$acf), aes(x=lag, y=corr)) + 
  geom_line() + ggtitle("ccf function")
p3 = ggplot() + geom_line(aes(x=-16:16, y=rr.sine)) + ggtitle("my intuition")
p1 + p2 + p3

# plot sines + ccf.sig
p1 = ggplot() + geom_line( aes(x=1:100,y=sin1)) + 
  geom_line(aes(x=1:100,y=sin2)) + ggtitle("sines 1 and 2")
p2 = ggplot(data.frame(lag=ccf.sine$lag, corr=ccf.sine$acf), aes(x=lag, y=corr)) + 
  geom_line() + ggtitle("ccf function")
p3 = ggplot() + geom_line(aes(x=-16:16, y=rr.sig)) + ggtitle("my intuition")
p1 + p2 + p3
R Greg Stacey
  • 2,202
  • 2
  • 15
  • 30
  • Your code clearly is incorrect, because if you have indeed lagged one function correctly, then the estimated correlation at that lag should be exactly $1,$ but your maximum correlation in the first example does not attain that value. Your task, then, is one of debugging rather than of changing your intuition. – whuber Mar 28 '20 at 13:32
  • @whuber Thanks. By "Your code clearly is incorrect" do you mean the ccf output (middle panels) or my custom code (right panels)? Since the usage of the ccf function is so simple I thought maybe the error was in my understanding of cross-correlation, especially since I only know the intuitive "sliding one vector" version of it. – R Greg Stacey Mar 28 '20 at 18:54
  • Just to be explicit, what are some expected behaviours of cross-correlation in my two examples? – R Greg Stacey Mar 28 '20 at 18:57
  • https://stats.stackexchange.com/questions/81754 explains the problem. – whuber Mar 31 '20 at 16:24

0 Answers0