Estimating prediction error and confidence band

Question

Like a lot of amateurs, I would like to see how well the evolution of Covid-19 is predictable. So I imported the data (here, for Italy) and fitted a logistic curve. Then I added the 90% and 95% confidence bounds. I got the following plot:

Great. The next day, I updated my plot with the latest data and realized that the estimation was had been quite optimistic and the asymptote is now much increased (same scale in both pictures):

Questions I understand that if the logistic model had been good, the next point should have been in the confidence range with a probability of 90% (or 95%). Can I conclude that the logistic model is not a good model here? Are there some standard procedures to assess the validity of the prediction by taking into account the uncertainty on the model?

Also, the difference between the two asymptotes gives me an indication of the precision of the prediction (it is not off by 1 or by 10^5 but by about 500 deaths). Is there some classic methods to take this into account?

Edit 21/03/2020: clarification in response to hakan's answer

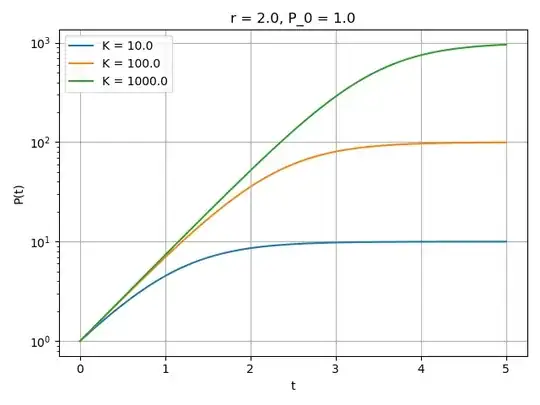
The model I fitted is $$\dfrac{c}{1 + a e^{-b x}}$$ and with $a=514434$, $b=-0.276$ and $c=5568$. Of course, this model is the same as @hakanc's, with a different parametrization (e.g. his $K$ corresponds to my $c$). The corresponding covariance matrix is $$\begin{bmatrix} 1.1\times 10^{10}& 641 & -2.5\times 10^7 \\ \star & 3.8\times 10^{-5} & -1.6\\ \star & \star & 80\times 10^3 \end{bmatrix}$$

I believe the low sensitivity to $c$ ($=K$) is described by the $(3,3)$ component of the covariance matrix, $\sigma=\sqrt{80\times 10^3}\approx 280$. So though I understand (and agree with) the argument of low sensitivity, I believe it is already included in the "confidence band".

Answer 1

When working with mathematical models, it is always good to check the assumptions of the model. The logistic function is often used when modelling population growth, and specifically where the rate of reproduction is proportional to both the existing population and the amount of available resources, all else being equal. Letting $P$ represent population size, the differential equation is

$$ {\displaystyle {\frac {dP}{dt}}=rP\cdot \left(1-{\frac {P}{K}}\right),} $$ where the constant $r$ defines the growth rate and $K$ is the carrying capacity, see the link for more details. The solution, letting $P_0$ be the initial population, is $$ P(t)={\frac {KP_{0}e^{rt}}{K+P_{0}\left(e^{rt}-1\right)}} $$ Thus, this model would be appropriate if Italy did nothing to mitigate the spread of the virus, but they are in fact using quarantine. The effect of wrong modelling assumptions would be that if you cross-validated the fitted model, you would get poor results.

Additionally, since the shape of the logistic function is

and in your data, it does not seem to include the part where the curve flattens out, I would suspect that the parameter describing that phenomenon, $K$, would have a high variance from your estimation procedure. An intuitive explanation for this can be done by plotting the function for different $K$ and constant $r$:

In this figure, if there is only data for $t$ between 0 and 1 would not reveal so much information on $K$, other than if $K$ is around 10, compared to $K > 100$. More formally, assuming you are doing maximum likelihood estimation, you can look at the eigenvalues of the Hessian of the corresponding likelihood function, to see if optimization problem is well conditioned.