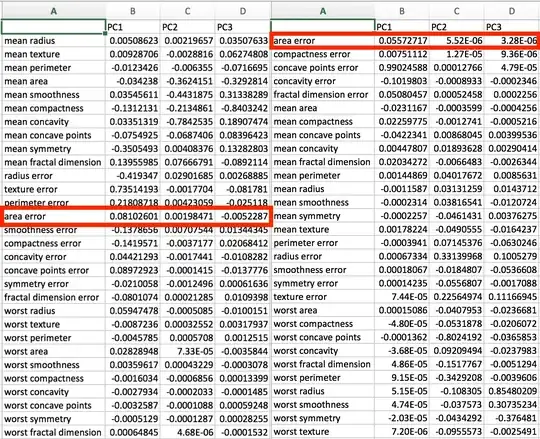
The rotation matrix outputted by the PCA algorithm should be independent of something trivial like the column ordering of the source data. Can anyone explain why my output diverges from my expectation for consistency?
I made a test input file 30x569 from a pre-made dataset
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
cancer.keys()
df = pd.DataFrame(cancer['data'],columns=cancer['feature_names'])
df.to_csv(r'input file',index=False)
Then generated a 30x30 output with all the covariance-based PCA components
import pandas as pd
import numpy as np
daily_series = pd.read_csv (r'input path')
sd = daily_series[daily_series.columns[0:daily_series.shape[1]]]
scaled_data = sd #unscaled
from sklearn.decomposition import PCA
pca = PCA(n_components=daily_series.shape[1])
pca_model = pca.fit(scaled_data)
components = ['PC1','PC2','PC3','PC4','PC5','PC6','PC7','PC8','PC9','PC10','PC11','PC12','PC13','PC14','PC15','PC16','PC17','PC18','PC19','PC20','PC21','PC22','PC23','PC24','PC25','PC26','PC27','PC28','PC29','PC30']
variables = daily_series.columns[0:daily_series.shape[1]]
Matrix = pd.DataFrame(pca_model.components_, columns=components, index=variables)
Matrix.to_csv(r'output path', index=True)
When I reorder the columns (let's say alphabetically) of the test input file. And run the above my output from the original test is different not just in the signs but also magnitude. I don't understand how that's possible.
Output (left is original output/right is output after alphabetizing columns in source data):