7

(This question is a bit related to a previous question of mine, but that question was about between subject comparison while this question is specifically about making inferences the group mean.)

When analyzing data using a hierarchical Bayesian model you sometimes don't want to make inferences on the individual subjects but rather on the group level (e.g. for girls aged 10 the most credible test score is 100 with a 95% credible interval of [75, 125]). When building such a model using an MCMC framework, for example JAGS/BUGS, I see two ways of getting at the group level mean. Either I can use the mean of the prior ($\mu_\text{gr}$ in the diagram below.) on the mean of the sampling distribution or, for each iteration of the MCMC algorithm I can calculate the mean of all the subject means (that is the mean of all $\mu_\text{subj}$ in the diagram below). If I want to make inferences about the group mean which of these two alternatives should I use?

As a test to see what happens when using the the two different alternatives I ran a model with simulated data.

Here is a Kruschke style diagram of a hierarchical model where we estimate the mean $\mu_\text{subj}$ for a number of subjects with a normally distributed group prior on $\mu_\text{subj}$ with mean $\mu_\text{gr}$.

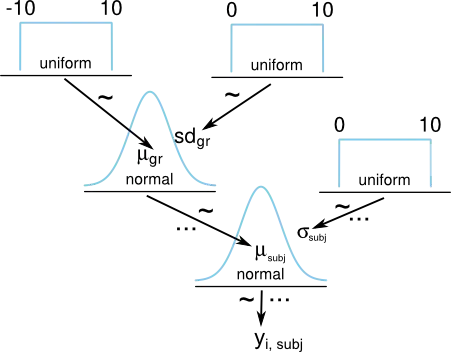
Kruschke diagram

Here is JAGS and R code for specifying the model above and simulating data for 50 subjects where each subject gets a mean that is randomly normally distributed with $\mu=0$ and $\sigma=1$. The JAGS model is then run for 5000 iterations and each iteration the mean of the prior, group_mu, and the calculated mean of the subjects, mean_mu <- mean(mu[]), is saved.

library(rjags)
model_string <- "model {
  for(i in 1:length(y)) {
    y[i] ~ dnorm( mu[subject[i]], precision[subject[i]])
  }

  mean_mu <- mean(mu[])
  for(subject_i in 1:n_subject) {
    mu[subject_i] ~ dnorm(group_mu, group_precision) 
    precision[subject_i] <- 1/pow(sigma[subject_i], 2)
    sigma[subject_i] ~ dunif(0, 10)
  }

  group_mu ~ dunif(-10, 10)
  group_precision <- 1/pow(group_sd, 2)
  group_sd ~ dunif(0, 10)
}"

# Creating fake data
n <- 10
n_subject <- 50
subject_mean <- rnorm(n_subject, mean=0, sd=1)
y <- rnorm(n * n_subject, mean=rep(subject_mean, each=n), sd=1)
subject <- rep(1:n_subject, each=n)

# Running the model with JAGS
jags_model <- jags.model(textConnection(model_string),
                         data=list(y=y, subject=subject, n_subject=n_subject), 
                         n.chains= 3, n.adapt= 1000)
update(jags_model, 1000)
jags_samples <- jags.samples(jags_model, 
                             variable.names=c("group_mu", "mean_mu"),
                             n.iter=5000)

Looking at quantiles and boxplots of mean_mu and group_mu show that they are both centered around the true group mean but they differ a lot in spread with the 95% credible interval being much wider for group_mu than for mean_mu.

quantile(jags_samples$mean_mu, c(0.025, 0.5, 0.975))
##       2.5%         50%       97.5% 
##  -0.10804263 -0.00741235  0.09216414 
quantile(jags_samples$group_mu, c(0.025, 0.5, 0.975))
##        2.5%          50%        97.5% 
##  -0.262734656 -0.008996673  0.248624938
boxplot(jags_samples, outline=F, horizontal=T)

enter image description here

So if I want to make inferences about the group mean which distribution should I use, group_mu or mean_mu? For me this is not clear and any explanation why one is to be preferred over the other is highly appreciated!

Community
  • 1
Rasmus Bååth
  • 6,422
  • 34
  • 57

2 Answers2

2

What has happened is that the estimates of the individual subject means have been shrunk towards the group mean, causing the std. deviation of the subject means (and consequently that of the mean of the subject means) to be "too small". This shrinkage is part and parcel of the hierarchical Bayesian approach. The group_mu values are the ones that you want.

You can see in a more empirical manner that the group_mu values are correct by comparing the width of the observed 95% credible interval from your quantile summary to the width of the confidence interval you would expect in classical statistics if you had directly observed the 50 true subject means. In this case, that's just $1.96/\sqrt{50}$, or +/- 0.28, which corresponds pretty well to the quantile results you displayed above for group_mu: (-0.26,+0.25). Since you can't do better than you could if you'd actually observed the 50 subject means, it follows that the credible interval shouldn't be much smaller than the confidence interval (as you're not adding any substantial prior information to the likelihood.) Clearly the (-0.1, 0.09) quantiles of the alternative mean are too close to 0, by this comparison.

In fact, you can use the ratio of the std. deviation of the mean of the estimated subject means to the std. deviation of group_mu as an index of how much shrinkage has taken place. (It's not the only such metric; I'm just pointing it out since you're calculating them both anyway.) If you have a very small ratio, that indicates, in a heuristic sense, that the hierarchical part of the model isn't adding much, and assuming all the subject means are the same may be a plausible alternative. Conversely, if the ratio is near one, that also indicates that the hierarchical part of the model isn't adding much, and just having a "fixed effects" model for the subject means would likely be almost as good - questions of modeling approaches etc. aside.

jbowman
  • 31,550
  • 8
  • 54
  • 107
  • Thank you for your answer! One reason for that I was asking is that I've seen examples where participants from two groups are modeled as coming from the same group (like the model above) but the two groups are then compared using a posterior that is created by taking the difference between the two groups for every step of the MCMC chain. This, to me, seems quite similar to taking the mean of the whole group for each step of the MCMC chain (as I have been doing above.) Intuitively, I would instead have defined different priors for the two groups and compared the posteriors of those priors. – Rasmus Bååth Dec 03 '12 at 09:39
  • Do you mean you would have defined different priors for the two models (no group difference vs. group difference)? In a case like that, though, you can, with some pain, use the Carlin and Chib approach to calculating Bayes factors (http://www.mrc-bsu.cam.ac.uk/bugs/winbugs/examples.shtml, the pines example), which assumes that one of the two models is actually correct I'm afraid. – jbowman Dec 05 '12 at 16:54
  • I rather meant that I define two hyperprios, one for each group (say mu_g1 ~ dnormal(...) and mu_g2 ~ dnormal(...)) and then see if mu_g1 - mu_g2 is credibly different from 0. – Rasmus Bååth Dec 06 '12 at 10:37
  • 1
    Have you considered using DIC as well? I tend to use DIC, LPML, and staring at a histogram of the difference between means more or less at once. – jbowman Dec 06 '12 at 17:00
0

If you wish to make inferences about the group level then your distribution of interest is $p(\mu_{gr}|Y)$. The simple reason is that $\mu_{gr}$ is actually a random variable in your generative model. Mean_mu is not a random variable in your generative model, it is a statistic that either your sampler happened to generate or you happened to compute. Furthermore, mean_mu is actually a point estimate of the posterior distribution of the true group mean, your distribution of interest. Point estimates provide less information than the full distribution, and you already have the full distribution itself (or at least a large number of samples that approximate it).

jerad
  • 1,239
  • 11
  • 14