Bias-Variance Trade Off with Cauchy Estimator

Question

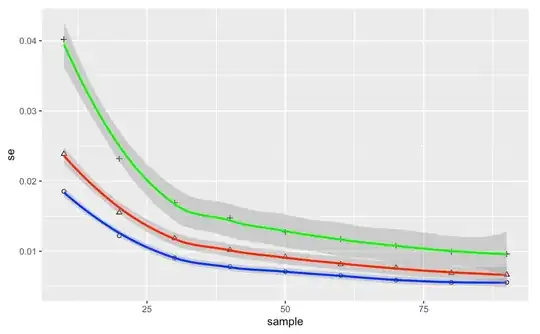
I'm having a look at the bias and standard error of a set of estimators. I expected to see the trade off when varying the parameter of the estimator, but I see that both the bias and the variance decline.

Estimators $\hat \theta=q_p-\tan[\pi(p-0.5)]$ of the location parameter in the Cauchy Distribution ($f(y)=\pi^{-1}{(1+(x-\theta)^2)^{-1}}$), where $q_p$ is a sample p-quantile with $p\in (0,1)$. Using $\theta=0$.

I've looked at three estimators of this kind, with p = 0.5, 2/3 and 0.75 in R. For each estimator I've used this code: ($p=2/3$ for instance)

master_0.6 <- data.frame(sample = NaN, EXPECTestimator = NaN, bias = NaN, se = NaN )

row <- 1
for (i in seq(from=10, to=90, by=10)){

  estimator0.6 <- data.frame(V1 = NaN)
  for(k in seq(1,1000,1)){
    estimator0.6[k, 1] <- (quantile(rcauchy(i,0), probs = 2/3) - tan(pi*((2/3) - 0.5)))
  }

  master_0.6[row, 1] <- i         
  master_0.6[row, 2] <- (sum(estimator0.6)/1000)
  master_0.6[row, 3] <- master_0.6[row, 2] - 0 
  master_0.6[row, 4] <- (sqrt(sum((estimator0.6 - master_0.6[row, 3])^2))/1000)

  row <- row + 1
}

For this $p=2/3$ estimator I've looked at nine sample sizes ($n=10,20,...,90$). At each sample size I've generated 1000 samples and applied the estimator to each sample, giving a vector with 1000 rows of the estimator at this sample size. Then I calculate the bias and variance of the estimator at this sample size. The same is done for all nine sample sizes, for each estimator.

Blue for $p=0.5$, Red for $p=2/3$, Green for $p=0.75$

I expected to see an inverse relationship between standard error and bias, such that the 2/3 estimator would be a good 'balance' and the desirable estimator. However, we see that the relationships is not so, making the p=0.5 estimator clearly more desirable.

Is this expected or have I made an error?

Answer 1

As a comment - note that the Cauchy distribution does not have a mean, so I interpret your reference to the mean as being to the location parameter of the Cauchy, which, due to the symmetry of the Cauchy, is also the median of the distribution.

With respect to bias: the sample median is an unbiased estimator of the population median, so you should not expect the sample median to have a higher bias than any other estimator. Considering the bias of a sample quantile as an estimator of the corresponding population quantile: bias is smaller in central quantiles than in extreme ones; see the accepted answer to Demonstration of sample quantile bias.

With respect to standard error: the asymptotic distribution of the sample quantile $\hat{q}$ estimator of the population quantile $q$ is Normal with mean $q$ and variance

$$ \frac{q(1-q)}{n \left[f\;\left(F^{-1}(q)\right)\right]^2} $$

Observe that both the numerator and denominator go to zero as $q \to \pm \infty$. Performing the requisite calculations for a range of values for $q$ and plotting them leads to:

avar <- function(q) q*(1-q)/(dcauchy(qcauchy(q))^2)
q <- seq(0.5,0.99, by=0.001)
av <- avar(q)
plot(log(av)~q, xlab="Quantile", ylab="log (Asymptotic variance)")

At least asymptotically, your variance increases with $q$ and so does your bias (in general). This leaves the median as your best estimator in both respects, although note that the median is not the most efficient estimator of the Cauchy location parameter; see the answers to Consistent unbiased estimator for the location parameter of $\mathcal{Cauchy} (\theta, 1)$ for more information on this topic.