3

I am quite new to GAM, I was trying various interactions in my GAM models, the individuals interactions and combined interactions are not coming up the same.

There are three variables which define my target variable. So I tried to build three GAM models taking each of the three variables as individual spline

gam_mod <- gam(Stickiness ~ s(Proxy_Perimeter_FT, k = 6), data = DATA, method = 'REML')
gam_mod <- gam(Stickiness ~ s(BB_FT, k = 6), data = DATA, method = 'REML')
gam_mod <- gam(Stickiness ~ s(CD1_FT, k = 6), data = DATA, method = 'REML')

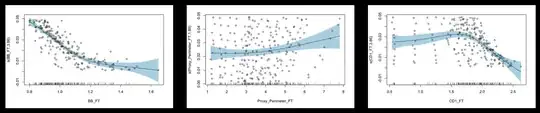
and plotting them I get these graphs. enter image description here

But when I am building GAM using all of the features, 

gam_mod <- gam(Stickiness ~ s(BB_FT, k = 3) + 
                            s(CD1_FT) + 
                            s(Proxy_Perimeter_FT), 
               data = DATA, method = 'REML')

I get this, enter image description here

Is it because that the variables might be interacting among each other as well that leads to GAM model producing these different graphs? Or maybe something else...

Any help would be highly appreciated, Thanks.

Dravidian
  • 133
  • 4
  • I think the core of the answer here is similar to this one: https://stats.stackexchange.com/a/400904/86176 "Coefficient estimates can change drastically based on which other variables are included in the model." – eric_kernfeld Dec 08 '19 at 22:12
  • This question is a duplicate of the following unanswered question. https://stats.stackexchange.com/questions/372997/linear-regression-coefficient-changes-with-additional-variables – eric_kernfeld Dec 08 '19 at 22:12
  • Also very similar to this one. https://stats.stackexchange.com/questions/61506/nonsignificant-interaction-still-causes-main-effect-to-flip – eric_kernfeld Dec 08 '19 at 22:14
  • Why does the raw data change between the two sets of plots? – JTH Dec 08 '19 at 23:01

1 Answers1

1

The most probable cause for what you are seeing is collinearity, i.e. your 3 independent variables are correlated.

Collinearity in Normal Linear Regression

One assumption of the linear regression is "no or little (Multi-)Collinearity". If we violate this assumption we get biased estimates (coefficients). Sometimes this is exactly what we want, e.g. confounder adjustment. Or we just don't care, like in predictive models (for this case regularization is advised, to handle potential problems due to collinearity and it's a good default choice).

To check this we calculate the linear correlation between the independent variables (in R: cor()). If the correlation coefficient for one pair is above 0.9 the model can become unstable and you should drop one of them. Any other non-zero correlation will introduce bias, but you should be careful with any correlations above 0.1.

I think it's even better to compare the univariate and multivariate coefficients, like you do. This also tells you which effect a correlation has (even if it is only 0.1). In my opinion this is something you should always do and in my field (epidemiology) reporting of raw and adjusted effects is strongly encouraged.

Collinearity in GAMs

The same assumption applies to GAMs. But now the collinearity assumption also applies to non-linear correlations (i.e. correlation between splines) and violations will change the whole spline function. The pearson (linear) correlation is now only an indicator and fails for highly non-linear relationships.

Again comparing univariate and multivariate estimates is a good choice. But if you want to dig deeper you can use GAMs to check the non-linear relationship between the independent variables. In your case:

gam_mod <- mgcv::gam(BB_FT ~ s(CD1_FT, k = 6), data = DATA, method = 'REML', select=TRUE)
summary(gam_mod)

The Summary function will give you multiple indicators to check if there is any non-linear relationship between the variables:

  1. F-Statistic: The higher the value the stronger the relationship after transforming the variable using a spline.
  2. The option select=TRUE performs variable selection and will drop the effective degress of freedom (edf) below 1, if there is only a weak relationship (also affects the F-Statistic). Any edf close to 0 means there is no relationship.
  3. "R² (adj.)" and "Deviance explained" both indicate no relationship if they are close to 0.

According to your images, CD1_FT and Proxy_Perimeter_FT seem to have a strong relationship. Maybe there is a subject-matter explanation.

Finally

There will always be some correlation between your independent variables. I think it's always good to know how the coefficients are changed in a multivariate model.

Example for no relationship

library(mgcv)
dat <- gamSim(1,n=400,dist="normal",scale=2)
b <- gam(y~s(x3),data=dat, method="REML", select=T)
summary(b)

Family: gaussian 
Link function: identity 

Formula:
y ~ s(x3)

Parametric coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)    7.910      0.193   40.99   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Approximate significance of smooth terms:
           edf Ref.df F p-value
s(x3) 0.001301      9 0   0.924

R-sq.(adj) =  -2.36e-06   Deviance explained = 9.02e-05%
-REML = 1108.1  Scale est. = 14.899    n = 400
ndevln
  • 303
  • 2
  • 7
  • This is a nice answer, but I am surprised to hear you say that any correlation among covariates leads to biased estimates. Assuming $Y = X\beta + \epsilon$ for iid gaussian entries of $\epsilon$, doesn't OLS give unbiased estimates of $\beta$ whenever $X$ is full column rank? $E((X^TX)^{-1}X^TY) = E((X^TX)^{-1}X^T(X\beta + \epsilon)) = \beta$. – eric_kernfeld Dec 08 '19 at 22:04
  • Yes. This is why I recommended comparing univariate and multivariate estimates as the method of choice. Do you know a better approach to check for this? – ndevln Dec 08 '19 at 22:53
  • Thanks for that elaborate response, its just that I had similar query as to what @JTH commented on the question. Why are the raw data points different? Is my understanding correct when I say that those datapoint reflect the effect of others variables as well, and are no longer raw datapoints? – Dravidian Dec 09 '19 at 15:01
  • 1
    Your data did not change as you can see from the x-axis rugs. The points represent residuals relative to your spline function (the y-axis represents the final regression coefficient). The variation of your residuals tends to decrease as you add more explanatory variables to your model. Also, the y-axis is the same for all plots from the multivariate model, which leads to a different perception. Your individual plots all have different y-axis ranges. In summary, your residuals are smaller and your plots are more zoomed out. – ndevln Dec 09 '19 at 17:47