How to recognize similar environmental variables using multivariate analysis?

Question

I am completely new to multivariate analyses and I need an advice how to get it applied to my data and which analyses to choose for which purpose.

My dataset is presence/absence (or relative abundance score) of 100 species on 5000 squares, and for each square I have 100 environmental variables (many of them strongly correlated).

1) Out of those environmental variables, how do I recognize which variables are similar with respect to species abundance? Which analysis to choose?

• By "with respect to" here I mean also non-linear functional dependence, because I intend use non-linear models (GP).
• By "similar" I mean they have similar effect in those general non-linear models.

2) Is it possible to get a distance matrix (matrix of distance between all pairs of environmental variables), which would express the similarity of those variables with respect to species abundance?

I was looking in R package vegan and the function vegdist() seems pretty close, but it's on the community data matrix - I need it for the environmental variables but with respect to the species abundance.

EDIT: I found my very amateurish way to do it, but I don't know if it's correct because I don't understand this properly (esp. the different scalings and transformations), so I would be grateful if a) you could check this and b) tell me better way how to do it:

1. I perform the CCA with species (community matrix) and environment.
2. I take the coefficients for variables that are centred and scaled to unit norm.
3. I scale (multiply) each dimension by appropriate eigenvalues of the environmental variables. I do this so that each dimension is weighted by its importance.

require(vegan)
c1 <- cca(df.sp, df.env) # species and environment data frames
cf <- coef(c1) # coefficients for variables that are centred and scaled to unit norm

# Now I will scale each dimension by the eigenvalues of the environmental variables so that each dimension is weighted by its importance:
cf.scaled <- cf*matrix(eigenvals(c1, model = "constrained"), nrow = nrow(cf),  ncol = ncol(cf), byrow = TRUE)

# finally compute the distance matrix:
di <- as.matrix(dist(cf.scaled))

EDIT 2: (response to the request of writing down the model). Very general description of the model would be:

$$\text{RelAbundance}_\text{species,square} \sim f(\textbf{Environment}_\text{square})$$

Where $\text{RelAbundance}_\text{species,square}$ is the relative abundance score (or just presence/absence) for given species and square, and $\textbf{Environment}_\text{square}$ is a vector of environmental variables for given square. $f$ is a general function of environmental variables.

Answer 1

Two features can be considered similar with respect to a response if they provide similar information about the response. In other words: if they're redundant for the purpose of predicting the response. I'll describe how to formalize this intuition using information theory, and use it to construct a measure of dissimilarity between features.

Proposed dissimilarity measure

Let $Y$ be a random variable representing the response (e.g. species abundance), and let $X_1,X_2$ be random variables representing two features (e.g. environmental variables). The conditional mutual information between $Y$ and $X_1$, given $X_2$ is:

$$I(Y; X_1 \mid X_2) = H(Y \mid X_2) - H(Y \mid X_1, X_2)$$

The conditional entropy $H(Y \mid X_2)$ quantifies our uncertainty about $Y$ when $X_2$ is known. Similarly, the conditional entropy $H(Y \mid X_1, X_2)$ quantifies our uncertainty about $Y$ when both $X_1$ and $X_2$ are known. So, their difference--the conditional mutual information--answers the following question: If $X_2$ is known, how much would our uncertainty about $Y$ be reduced by also being told $X_1$? Stated another way: how much information does $X_1$ provide about $Y$ beyond what $X_2$ already provides?

Similarly, we can ask how much additional information $X_2$ provides about $Y$, beyond $X_1$. This is given by the conditional mutual information between $Y$ and $X_2$, given $X_1$:

$$I(Y; X_2 \mid X_1) = H(Y \mid X_1) - H(Y \mid X_1, X_2)$$

I suggest the following measure of dissimilarity between $X_1$ and $X_2$ with respect to $Y$:

$$I(Y; X_1 \mid X_2) + I(Y; X_2 \mid X_1)$$

How it behaves

This dissimilarity will be low when $X_1$ and $X_2$ provide mostly redundant information about $Y$. In this case, $H(Y \mid X_1,X_2)$ will be only slightly lower than $H(Y \mid X_1)$ and $H(Y \mid X_2)$, since neither feature adds much to our knowledge about $Y$ beyond that provided by the other feature. So, $I(Y; X_1 \mid X_2)$ and $I(Y; X_2 \mid X_1)$ will both be low. In the extreme case where $X_1$ and $X_2$ provide perfectly redundant information about $Y$ (or are both completely uninformative), our dissimilarity measure will be zero.

On the other hand, dissimilarity will be high when $X_1$ and $X_2$ provide different information about $Y$. In this case, $H(Y \mid X_1, X_2)$ will be considerably lower than $H(Y \mid X_1)$ and $H(Y \mid X_2)$, since knowing both features tells us more about $Y$ than either feature alone. So, $I(Y; X_1 \mid X_2)$ and $I(Y; X_2 \mid X_1)$ will both be high.

Now, consider a case where $X_1$ is highly informative about $Y$ but $X_2$ is not. $H(Y \mid X_1,X_2)$ will be close to $H(Y \mid X_1)$, since $X_2$ tells us little about $Y$. So, $I(Y; X_2 \mid X_1)$ will be low. But, $H(Y \mid X_1,X_2)$ will be considerably lower than $H(Y \mid X_2)$, since $X_1$ tells us a lot about $Y$. So, $I(Y; X_1 \mid X_2)$ will be high, and the two features would be considered fairly dissimilar.

Properties

The proposed dissimilarity measure has the following properties:

• Symmetry. Dissimilarity between $X_1$ and $X_2$ is equal to that between $X_2$ and $X_1$.

• Nonnegativity. This follows from the fact that $H(Y \mid X_1,X_2)$ must be less than or equal to both $H(Y \mid X_1)$ and $H(Y \mid X_2)$. Intuitively, knowing an additional feature can't reduce our uncertainty about $Y$.

• The dissimilarity of a feature with itself is zero. But, the converse is not true; zero dissimilarity doesn't imply that two features are identical. It implies that they provide completely redundant information (or lack of information) about $Y$.

Notes

The information theoretic quantities used above allow for nonlinear, probabilistic dependence of $Y$ on $X_1$ and/or $X_2$. So, they can capture any kind of relationship. This flexibility is a desirable property. But, it has a price, in that estimation of entropy from sampled data can be challenging. Definitely consult the entropy estimation literature.

To obtain a dissimilarity matrix, simply calculate the dissimilarity measure between all pairs of features. Given the properties described above, this matrix will be symmetric and have zero diagonal. So, it suffices to compute the lower or upper triangle of the dissimilarity matrix.

Answer 2

Summary: Standard triplots for ecological data analyzed by canonical correspondence analysis (CCA*) provide a way to gauge both the strengths of relationships of individual environmental variables to species distributions and the similarities among environmental variables in these respects. You might, however, want to do some dimension reduction on the set of 100 environmental variables first, to minimize problems from multicollinearity and overfitting. Finally, some modifications to CCA can accommodate nonlinearities in the environmental variables, which might simplify your project overall.

Sources: This is outside my present expertise, but I find myself facing similar issues in my own work. I wrote this answer in large part to start learning about this. Most of the below is based on The Ordination Web Page (OWP), Multivariate Analysis of Ecological Data (MAED), and Correspondence Analysis in Practice (CAiP). Those sources should provide enough background in multivariate analysis for you to work effectively with a statistician having experience with this type of analysis.

Details:

Triplots:

Correspondence analysis (CA) can be considered a singular-value decomposition (SVD) of a transformed count matrix, say of species versus sites (your squares). The count for each species/site element of the matrix is first divided by the total number of counts for all species and sites. Then the matrix is standardized: expressed as residuals of these values from what would be expected if species and sites were independent, and weighted with respect to the total numbers for each site and each species. SVD of this matrix of standardized residuals provides the CA. Typically the first 2 principal coordinates (with highest singular values/eigenvalues) are selected, and values for species and sites are plotted with respect to those principal coordinates in a 2-dimensional display. This provides a way to combine information among species based on their relative distributions among sites, overcoming some concerns raised in comments.**

CCA, canonical correspondence analysis, takes this a step further by incorporating information about covariates (environmental variables) associated with each of the sites. The matrix of standardized residuals for species versus sites is regressed against the covariates (centered to 0 and normalized to unit standard deviation), restricting analysis to a "constrained" subspace that can be expressed as exact linear combinations of the covariates. SVD of this constrained subspace provides the CCA.

Now all 3 of species, sites, and covariates can be displayed with respect to the first 2 principal coordinates, providing a triplot. The contributions of the covariates can be represented as arrows, starting at the origin and ending at points proportional to their regression coefficients with respect to these 2 dimensions. This example comes from OWP:

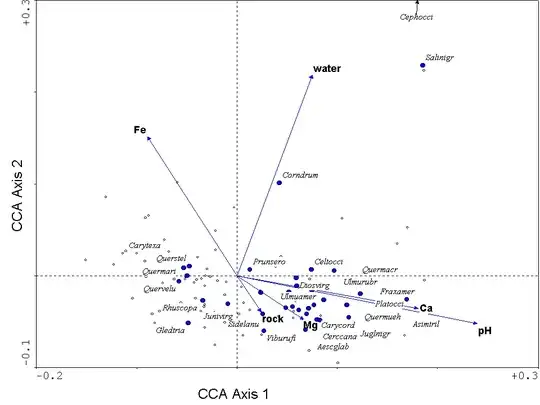
This provides the outline of a solution to your problem: the relative Euclidean lengths of the arrows represent the relative importances of covariates in terms of the species/site associations (within these dimensions of the constrained subspace). The angles between arrows represent dissimilarities among the covariates. In this example, Ca and pH are highly similar in angles, both are nearly orthogonal to water, and close to opposite in direction from Fe. So cosine similarity provides a straightforward basis for evaluating similarity among covariates. Although displayed here for 2 dimensions of CCA, you could determine Euclidean lengths and cosine similarities in as many dimensions as you choose to include in your analysis.***

Dimension reduction

The maximum dimension of CA is one less than the minimum of the number of sites or species (as the division of each individual original count value by the sum of all count adds one linear dependence). For CCA that dimension is reduced to the number of covariates, which in many examples is less than either the numbers of species or sites. In your case, however, the 100 environmental variables are similar to the number of species; as you note, many of those variables are highly correlated. I would fear problems arising from multicollinearity and overfitting in this case.

You probably should start with some unsupervised dimension reduction first, choosing individual variables that stand in pretty well for other variables (as suggested in references noted above) or doing a principal-components analysis on the environmental variables first and using a selection of principal components as the covariates to include in the CCA. (That would be the equivalent of principal-components regression for the regression component of CCA. It would seem that there should be a way to reduce dimension by penalizing covariates similarly to ridge regression or LASSO for this application, but a quick initial search didn't find anything.)

Modifications to CCA

The covariate values can of course be nonlinearly transformed appropriately (e.g., logarithmically) before incorporation into CCA. Chapter 15 of MAED shows that continuous covariates can be modeled by "fuzzy coding" into categorical variables, in a way that can accommodate more complicated non-linear relationships directly. It also seems that it should be possible to incorporate direct modeling of nonlinear relationships, say via restricted cubic splines, in the regression part of CCA; I haven't yet looked into that.

---

*For simplicity I use CCA as the abbreviation for canonical correspondence analysis here. Note that "CCA" is also used for canonical correlation analysis, a different type of multivariate analysis. To avoid confusion, I would recommend removing the "CCA" tag from this question, or editing the "CCA" tag info on this site to note the potential confusion.

**In a comment to an answer on a related question, I suggested that a multivariate partial least squares (PLS) approach might work for this situation. You might still consider that, but it would not provide any useful way to combine information among species. For a single-species analysis as in that other question there is no way to separate out relationships of environmental variables to species versus sites, so PLS still seems to be a good approach in such cases. Note, however, that single-species analysis is likely to be much less powerful than the multivariate analysis provided by CCA.

***You might have to get into the details of the implementations of CCA to extract the relative lengths and angles corresponding to the covariates. That would be off-topic on this site. Note that R packages provide source code, and there seems to be a mailing list for questions on ecologic analysis in R.

Answer 3

So one caveat, there are a lot of different ways to go about this, and it really depends on your field. That being said, there are some general principles for variable selection. Instead of using a distance matrix (which can be really really hard to view with 100 variables), I would suggest heading right to a model selection method, like stepwise model selection in R. Stepwise selection uses the Akaike information criterion (AIC):

$AIC = n \log(\sigma^2) + 2k$

Where $\sigma^2$ is the residual sum of squares and $k$ is the number of model parameters. Other formulations do exist. The general idea is that it penalizes the model for having more variables while rewarding it for better fit (measure by a smaller residual sum of squares). The theory for the exact formula is pretty heavy Phd in stats stuff, but hopefully that gives you a general idea.

Stepwise selection starts with either an empty model:

$Y = 1$

Or a model with all your variables:

$Y = \beta X_1 + \beta X_2 + ... + \beta X_{100}$.

It then attempts to either add or remove variables one by one to the starting model until it finds a better model (models with smaller AIC are considered "better"). After it selects which variable to add or subtract, it then goes through the same process again and again, either adding or subtracting one variable at a time until it cannot find a model with a lower AIC.

You can check out this article for a more substantive explanation and some R code.

This doesn't necessarily fix your your correlation issue. One very crude rule-of-thumb is that if two variables are correlation > .9, select the one that is more correlated with the response variable and throw out the other. Its a very crude rule of-thumb, but it will solve any massive problems.

This is a really complex problem you're trying to solve. It's the kind of problem where a lot could go wrong and a lot of different methods could be used, so I would highly suggest finding someone with some graduate level experience in regression to look at your data.