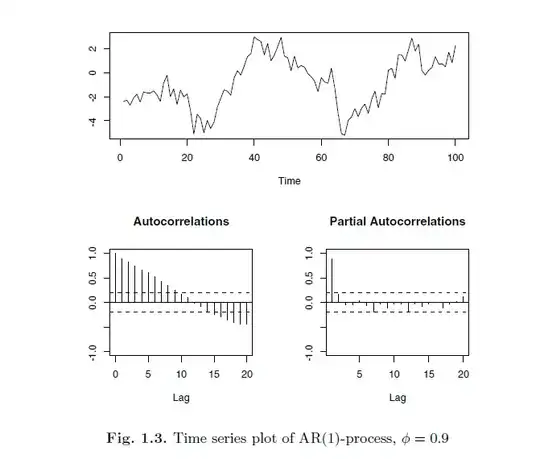
I am learning about this AR process. According to the book I'm reading, the autocorrelatio function of a stationary process: $$y_t = c + \phi y_{t-1} + \varepsilon_t, \quad \quad |\phi|< 1$$
is as follows: $\rho(h)= \frac{\gamma(h)}{\gamma(0)} = \phi^h$
Which means a slow exponential decay for successive lags, hence revealing that the series does behaves as an AR(1) process. So, I can not understand why in this case the autocorrelation function drops but then grows again.
set.seed(123456)
y <- arima.sim(n = 100, list(ar = 0.9), innov=rnorm(100)) `
op <- par(no.readonly=TRUE)
layout(matrix(c(1, 1, 2, 3), 2, 2, byrow=TRUE)) plot.ts(y, ylab='')
acf(y, main='Autocorrelations', ylab='', ylim=c(-1, 1), ci.col = "black")
pacf(y, main='Partial Autocorrelations', ylab='', ylim=c(-1, 1), ci.col = "black")
par(op)
Any explanation?