1

I am analysing a data set that is created from walking transects and recording counts for each group size of animals observed. Each transect has 41 repeats, which was approximately 80% zeros. However, within the actual observations, the counts also vary greatly with a large number of small group sizes but some >60 individuals as well.

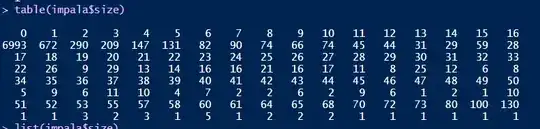
I want to analyse these data to determine the type of habitat that is preferable to this species by modeling the count data against the environmental covariates that occur at each transect. I have begun with a logistic regression, for which I converted to a logistic vector for all surveys where 1=presence and 0="pseudo absence". The raw count frequencies are as in the screenshot (sorry I didn't know how else to export this without creating a mess of numbers)

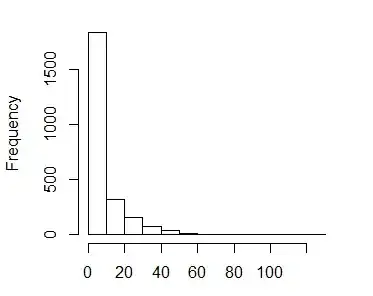
enter image description here

I would now like to look at a finer scale of how the preference of habitat varies among the habitats indicated with a higher proportional "selection" from the logistic regression model. Thus I subsetted the data to just the observations (counts>0). Which have the following distribution (x-axis is group size)

enter image description here

I suspected even without zeros these data were overdispersed I read up on this post and after trying the odTest and @BenBolker's own brand I determined they were.

overdisp_fun <- function(model) {
          rdf <- df.residual(model)
          rp <- residuals(model,type="pearson")
          Pearson.chisq <- sum(rp^2)
          prat <- Pearson.chisq/rdf
          pval <- pchisq(Pearson.chisq, df=rdf, lower.tail=FALSE)
          c(chisq=Pearson.chisq,ratio=prat,rdf=rdf,p=pval)
}

 overdisp_fun(mNB)
       chisq        ratio          rdf            p 
217168746.02     88351.81      2458.00         0.00

Where the mNB object was produced from the following model:

mNB<-glmer.nb(size~scale(Acacia.sp)
        + (1|TransectID)
        , glmerControl(optimizer = "bobyqa", optCtrl = list(maxfun = 100000))
        , na.action = na.fail
        , weights = w    # a weighting to account for detectability
        , data=imp.NB)

Which always returns the following singularity warning:

boundary (singular) fit: see ?isSingular

Which I am quite sure is bad news! so I was not surprised to see the high level of overdispersion. I have tried a number of combinations to vary the model's complexity. I have also run a glm.nb which was able to converge but I would prefer to include the random effects to account for the multiple samples taken from the same transect.

I would like to ask if anyone out there might have an idea for what I could try next to improve the fit for these data while including the mixed effects and accounting for the overdispersion.

EDIT

After process of elimination, I have found that the culprit causing the singularity issue is the weights argument which indicates a vector with values from 4.350753 to 6.992258. In most cases when the weight is removed, the model converges. Can anyone explain why and possible remedies?

I also have a question relating to this topic here

Nebulloyd
  • 253
  • 1
  • 6
  • 2
    link for a similar problem that shows one strategy for overcoming singularity https://stats.stackexchange.com/questions/30465/what-does-a-non-positive-definite-covariance-matrix-tell-me-about-my-data Check the first reply by Michael Chernick. Essentially, you have a situation in which determinant of a square matrix is zero. This is telling you that you have some sort of linear dependency. So, one possible resolution would be to build model by sequentially adding variables, until you hit the problem of singularity. Then you could make a judgement call as to which variable to retain. – PsychometStats Oct 24 '19 at 17:02
  • @PsychometStats thanks for the suggestion. Unfortunately, I have already tried this. No matter which covariate I use I get a run of the same singularity warning. I have also tried using year and season as random effects to see if that was the problem but it just keeps throwing the same thing. Using `vcov` for the above model I get values really close to zero for both (`5e-5` `4e-6`)...any ideas? – Nebulloyd Oct 24 '19 at 21:02
  • Actually I just realised that the covariation between the intercept and Acacia.sp is negative. So `-5e-5` – Nebulloyd Oct 25 '19 at 15:10
  • 1
    I’d be curious to know what the variance for your random intercepts looks like with and without the weights. – Matt Barstead Oct 26 '19 at 23:44
  • @MattBarstead I get 0 and 0.1079 with and without, respectively. `ranef(mNB)` shows 0 for all transect ID values when weights are added... – Nebulloyd Oct 27 '19 at 22:23
  • 1
    So without actually having your data to play with, what seems like is happening is that your weights are accounting for 100% of your random effect variance, and so after weighting, you have no random intercept variance left for the model to chew on. – Matt Barstead Oct 27 '19 at 23:03
  • 1
    What exactly goes into your weight value? – Matt Barstead Oct 27 '19 at 23:06
  • The weights should compensate for imperfect detection during the survey, modeled as probabilities in ‘Distance’. They have been rescaled (1-10). 1 represents observations in habitat with the highest chance of detection, and 10 should give observations in habitat with the lowest chance of detection greater weight. In the case of this species, I think the values go from 3-7. Not sure if an easy way to replicate the characteristics of this data set which has 2700 observations but will happily post it somewhere if you’re interested? – Nebulloyd Oct 28 '19 at 17:43

0 Answers0