0

So I've got a response variable with count data e.g. number of species found and two explanatory. The first is a treatment I did or did not applied -> Yes or No, so binary. My second explanatory would be continuous. I want to check for the dependencies.

lm will not work for this data, so I want to try a glm in R:

glm(responsecount~explanatorycontinuous+explanatorybinary+explanatorycontinuous:explanatorybinary,data=File1)

but which correction should I chose binomial or poisson (and which link) and why?

The experiment is staged and the decision about herbicide treatment is determined at random. There are fields with and without herbicide and every field has multiple plots in which the number of species was counted.

This is the plot for my data,so you can see the distribution of my datapoints:

EdM
  • 57,766
  • 7
  • 66
  • 187
Kaly
  • 9
  • 2
  • 1
    You seem to use "binomial" in multiple distinct ways: is that intentional? For instance, you appear to use it in the second sentence as a synonym for "binary." Because your question focuses on whether a response distribution should be modeled as "binomial," perhaps you ought to state what you think this means. – whuber Oct 03 '19 at 18:19
  • 2
    Your "explanatory count" variable seems to be a continuous variable (distance to the field) that you sampled at 8 different values in your study. Usually the phrase "count variable" means something that can _only_ take on non-negative integer values, like your "number of species" response variable. Perhaps in your scale of measurement the "distance to field" only takes on integer values, but it would still be considered "continuous." To reduce confusion for those who might read your question in the future, please edit your question to clarify both this issue and the one noted by @whuber. – EdM Oct 03 '19 at 18:31
  • @whuber My lecturer always referred to binomial so i thought Yes and No must be binomial. I changed it to binary now. Thanks for the advice – Kaly Oct 03 '19 at 18:41
  • @EdM Your right it could be negative too. I did not thought about it. Thank you. – Kaly Oct 03 '19 at 18:44
  • 1
    Thanks for updating the question. Your plot doesn't seem to show any cases in which the number of species was 0. Is that correct, or is that just an artifact of how the data are plotted? (Also, thanks for showing the plot--it makes it much easier to try to give a good answer.) – EdM Oct 03 '19 at 18:56
  • @ EdM Yeah it is correct, I counted at least one species. – Kaly Oct 03 '19 at 19:07
  • Is this a planned experiment? How was it decided to use or not the herbicide treatment? – kjetil b halvorsen Oct 03 '19 at 23:47
  • @kaly: new information should really be edited as part of the question, please! Your description makes this look like a split-plot experiment. Can you please give full details on the experimental design? How many plots in each field? ... – kjetil b halvorsen Oct 04 '19 at 09:39

1 Answers1

1

When you fit a generalized linear model, you must specify two things. First you specify a distribution family* that describes how the variance of outcome values changes with their mean. Second, you specify a link function that describes how the linear-predictor values from the model correspond to mean outcome values.

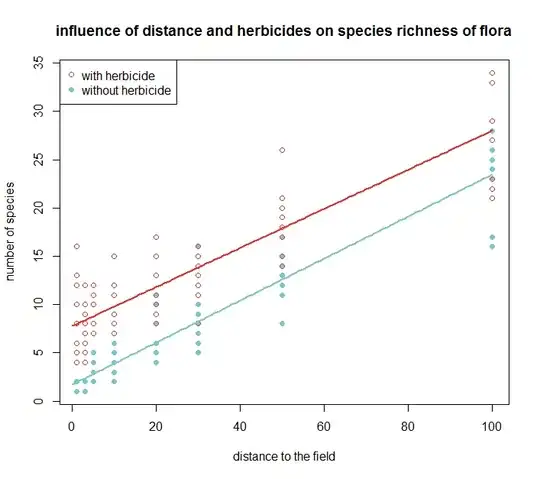
For count values, the Poisson family is a standard initial choice; the binomial family is generally reserved for yes/no or success/failure types of outcomes. For the Poisson family the variance equals the mean. That said, i'm a little concerned about whether your data will be well represented by the Poisson, as you have no 0 values even at low mean response counts. For example, the two "without herbicide" sets of cases with smallest "distance to the field" values have mean counts of about 1.5. A Poisson distribution with a mean value of 1.5 should have 0 counts in about 22% of cases, so you might need to consider an alternative.

The fitted regression model provides a combined linear predictor value for any specified values of your predictor variables. For example, say that your model has an intercept $\beta_0$ for the case without herbicide and 0 "distance to the field," a slope $\beta_1$ with respect to "distance to the field," and a fixed effect $\beta_2$ of "herbicide" independent of "distance to the field" (no interaction). Call "distance to the field" $d$ and the "herbicide" predictor $h$ with a value of 0/1 without/with herbicide. The the linear predictor for any specified $d$ and $h$ values would be $\beta_0 + \beta_1 d + \beta_2 h$. The link function is chosen to map the linear-predictor values to predicted mean values of responses. According to your plot, it looks like the mean observed counts change directly with respect to such a linear predictor, so a choice of an identity link rather than the R default log link could be reasonable.

As with any regression, it is important to check how well the model fits the data and to amend the model accordingly. That might end up requiring different choices of distribution family and link function.

I think that both @kjetil b halvorsen and I have some additional concerns about your specific experimental design, depending on which there might be some additional terms required in the formulation of your model, perhaps including a random effect, to account for potential correlations among observations. The above, however, should help clarify your choices of distribution family and link function in any event.

*You call this a "correction" in your question. Again, it helps to use the agreed-on terminology. Visiting this site can help you learn the terminology if your courses are somewhat deficient in that respect.

EdM
  • 57,766
  • 7
  • 66
  • 187