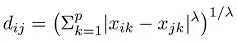I wanted to confirm my intution about the meaning of "loadings" I have made out of eigenvalue/eigenvector decomposition, but I still fail to do that.
Note that I made 3 pairs of highly correlated variables, expecting 3 'significant' principal components, and it works as expected.
However, when I build the loadings I get a plot that does not show me three distinct correlation peaks.
Why don't I get a clear picture showing variable clustering in terms of correlation with the scaled components (let them call factors loosely)?
Can I do different analysis to have what I want (prcomp / factanal)?
set.seed(1)
x1 = rnorm(1000)
x2 = x1 + rnorm(1000, 0, 0.2)
x3 = rnorm(1000)
x4 = x3 + rnorm(1000, 0, 0.2)
x5 = rnorm(1000)
x6 = x5 + rnorm(1000, 0, 0.2)
dt <- data.frame(cbind(x1,x2,x3,x4,x5,x6))
A <- as.matrix(dt)
ei <- eigen(cov(A))
eivals <- ei$values
plot(eivals)
eivecs <- ei$vectors
loading_1 <- eivecs[,1] * sqrt(eivals[1]/sum(eivals))
loading_2 <- eivecs[,2] * sqrt(eivals[2]/sum(eivals))
loading_3 <- eivecs[,3] * sqrt(eivals[3]/sum(eivals))
plot(loading_1, type = 'l', ylim = c(-1,1), ylab = 'loadings', xlab = 'variables'); lines(loading_2, col = 'red'); lines(loading_3, col = 'blue'); axis(1, at = 1:6, labels = paste0('x', 1:6))
Update (2019-10-07)
I have obtained a much cleaner picture here after rotation.
My question transforms now to:
whether I can take (for example) modulus of these loading coefficients to be able to treat the figures as correlation coefficients of variables with factors? I cannot describe neither to colleagues nor to myself what the negative relation means.
I try to do topic modelling, where variables are word frequencies, by the way. So said, I would love to say that this topic (factor) is dominated by Russia (0.7), politics (0.71), and another topic by Economy (0.72), Oil (0.69).
## PCA + Varimax
set.seed(1)
x1 = rnorm(1000)
x2 = x1 + rnorm(1000, 0, 0.2)
x3 = rnorm(1000)
x4 = x3 + rnorm(1000, 0, 0.2)
x5 = rnorm(1000)
x6 = x5 + rnorm(1000, 0, 0.2)
dt <- data.frame(cbind(x1,x2,x3,x4,x5,x6))
M <- as.matrix(dt)
prc <- prcomp(M)
loading_1 <- prc$rotation[,1]
loading_2 <- prc$rotation[,2]
loading_3 <- prc$rotation[,3]
plot(loading_1, type = 'l', ylim = c(-1,1), ylab = 'loadings', xlab = 'variables');
lines(loading_2, col = 'red');
lines(loading_3, col = 'blue');
axis(1, at = 1:6, labels = rep('', 6));
axis(1, at = 1:6, labels = paste0('x', 1:6))
## Varimax
L <- prc$rotation[,1:3]
R <- varimax(L, normalize = TRUE, eps = 1e-5)
R$loadings
loading_1 <- R$loadings[,1]
loading_2 <- R$loadings[,2]
loading_3 <- R$loadings[,3]
plot(loading_1, type = 'l', ylim = c(-1,1), ylab = 'loadings', xlab = 'variables');
lines(loading_2, col = 'red');
lines(loading_3, col = 'blue');
axis(1, at = 1:6, labels = rep('', 6));
axis(1, at = 1:6, labels = paste0('x', 1:6))