I know it is said that we do the reparameterization trick so we can do back-propagation and back-propagation cant be applied on random sampling!
However, I don't precisely understand the last part. Why cant we do that?
We have a mu and a std and our z is directly sampled from them. What is the naive method that we don't do ?

I mean what were we supposed to do that didn't work and instead made us do reparameterization?
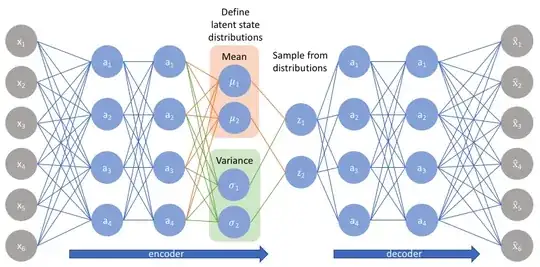 we had to sample from the distribution using mean and std, any way, and we are doing it now, whats changed?
we had to sample from the distribution using mean and std, any way, and we are doing it now, whats changed?
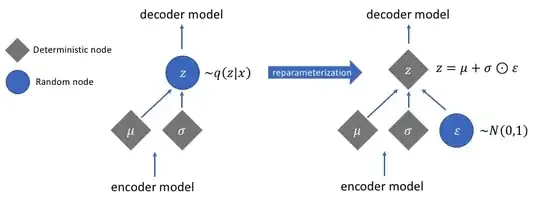 I dont get why z in is considered a random node previously, and not now!?
I dont get why z in is considered a random node previously, and not now!?
I'm trying to see how the first way is different than what we are doing in the reparameterization and I cant seem to find anything!