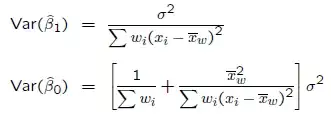everyone!
I'm digging in meta-regression and doing hand calculations using WLS to get better understanding of the topic. I'm fine with calculations for univariative model (that is, 1 covariate is considered) but faced problems when several predictors are considered. I use following formulas for univariative model:
1. intercept and slope
2. variance for intercept, slope, and corresponding mean squared error
3. F-test for estimation of between-study variance in random-effects model
*w - weight; y - outcome; x - predictor
My question is how should I modify and extend these formulas for multivariative case when two, three, and more predictors are accounted for? In particular, formulas for variance and F-test are of interest (I guess, covariance is supposed to be incorporated there).
The available infromation on Internet consideres this topic in matrix form, but I ask for the answer in scalar form (not a mathematician, unfortunately).
Thanks in advance for any help.