I'm not an ML scientist, but I'm trying to understand how variational autoencoder works.
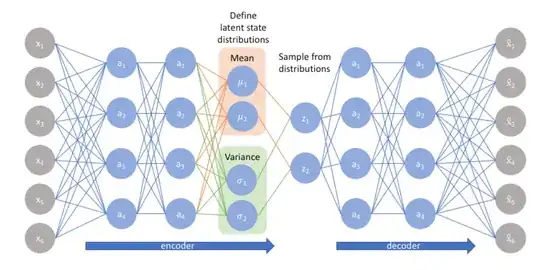
I'll take as reference the following diagram, which it couldn't be used for backpropagation as includes a sampling process but it captures anyway what I don't understand. The diagram is taken from this link.
I'm specifically going to focus on the encoder part. My understanding is that $x_1,\ldots, x_6$ are real values (the features) and in the second layer each of $a_1, \ldots\ a_4$ is another real value.
No we have these functions $\mu_1,\mu_2,\sigma_1,\sigma_2$, from that diagram again it seems that both $\mu_1$ and $\mu_2$ compute the mean of the vector $a = (a_1,\ldots,a_4)$ but if this is the case then $\mu_1(a) = \mu_2(a)$ and I don't see the point of this, I'd make a similar observation for the $\sigma_1, \sigma_2$ functions.
The question is, w.r.t. that diagram, how exactly are $\mu_1$ and $\mu_2$ computed?