3

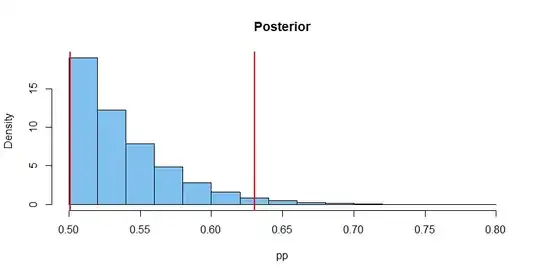
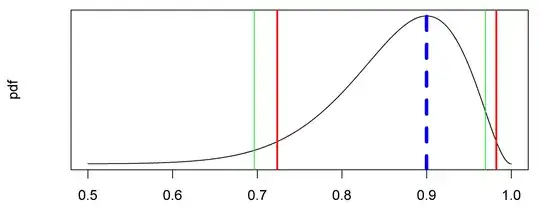
A standard problem is estimation of confidence intervals for a population proportion given that one has observed f successes out of n independent trials. There is a reasonable discussion of this problem at https://en.wikipedia.org/wiki/Binomial_proportion_confidence_interval and several R packages perform the calculation using a variety of methods (e.g. binom.confint in the package binom or bintol.int in the package interval). My problem is similar except that I know for certain that the population proportion lies in the range 0.5 to 1; within that range a uniform prior would be appropriate, although I am not wedded to a Bayesian approach. Of course particular small samples may nevertheless yield fewer successes than failures. Sample sizes are typically 10-30 trials, occasionally lower.

Ideally I would like an R function or some lines of code that would generate appropriate confidence limits. Otherwise some advice about other approaches (e.g. online calculators, programming in C) would be appreciated. My probability theory is rusty!

The motivation for this is analysing some genetic crosses following the rules of Mendelian genetics. I am crossing a heterozygote female with a homozygote recessive male and then with a homozygote dominant male. If the first male fathers all offspring, one expects a roughly 50:50 ratio of phenotypes (equal numbers of double recessives and hetoryzgotes); if the second male fathers all offspring, they will all exhibit the dominant phenotype. But sperm from both matings may be used, so any intermediate proportion between 0.5 and 1 is possible. This seems like a standard problem in genetics, which is what leads me to expect that there is a ready-made solution out there.

Many thanks!

hutch
  • 61
  • 3

2 Answers2

2

Suppose you have 20 trials and observe 5 successes. Using your prior, the following R code gives a 95% Bayesian posterior interval $(.501, .630)$ for the proportion of successes. Another run with a different seed gave $(.501, .629).$ [Maybe for fewer than 10 successes, you'd prefer a one-sided 95% interval, $(.5, .609).]$

 set.seed(815)
 m = 10^7
 p = runif(m, .5, 1)  # prior
 x = rbinom(m, 20, p)
 pp = p[x == 5]
 length(pp)
 [1] 12951            # sufficient nr of cases
 hist(pp, prob=T, col="skyblue2", main="Posterior")
 q = as.numeric(quantile(pp, c(.025,.975)));  q
 [1] 0.5011254 0.6304784
 abline(v=q, col="red", lwd=2)

enter image description here

If you got 18 successes in 20, then the Bayesian interval would be $(0.696, .970)$ and a frequentist Agresti-Coull interval $(0.684, .982).$

enter image description here

BruceET
  • 47,896
  • 2
  • 28
  • 76
  • Solution is neat and understandable: great! But 2-tailed vs 1-tailed issue bothers me. When successes/trials is < 0.5, a 1-tailed CI makes sense. But also when successes/trials = 0.51: a 2-tailed CI excludes p=0.5, which is silly. 2-tailed CIs are appropriate when well away from 0.5 and 1, but if successes/trials=0.99, again a 1-tailed CI seems right. Shouldn’t we shift how much of the 5% is in each tail outside the CI depending on the nearness of successes/trials to 0.5 and 1? This must be a standard problem: what’s the phrase to search for? Or even can you suggest more nice code? – hutch Aug 15 '19 at 17:44
  • You asked for a 95% CI; I assumed you meant a 2-sided CI. Sometimes when the lower limit of a CI comes very close to a boundary of permissible values, people like to use one-sided CIs. But usually, people make 'probability symmetric' two-sided CIs, putting half of the error probability in each tail. Sometimes with asymetrical dist'ns, such as exponential, people search for the allocation of probabilities in the tails that produces the shortest CI.(Also, when doing one-sided tests, it is customary to use one-sided CIs.) Recognizing variations, one usually speaks of "**a** 95% CI" not **the.** – BruceET Aug 15 '19 at 18:30
  • Mainly, I took followed your lead to discuss probability intervals based on posterior distn's. One style of interval is HPD (highest probability density). That would pick 95% of probability where posterior density is largest, also usually the shortest. Using my code you only have an estimate of posterior density. Maybe the idea will lead to what you're hinting at a couple of Comments before. // When the point est is < 1/2, HPD is close to one sided. – BruceET Aug 15 '19 at 21:04
  • Helpful. Further useful discussion at https://stats.stackexchange.com/questions/4713/binomial-confidence-interval-estimation-why-is-it-not-symmetric. If I minimise width of CI, the relative sizes of the 2 tails shift as I want. This code added to yours achieves this: alpha 1-tail;~0.5=>symmetric – hutch Aug 15 '19 at 21:17
1

Having learnt the principle from BruceET's answer, I have created another version that avoids simulation. Instead I use dbinom() to calculate the probabilty of getting the observed result over a regularly spaced array of p values. These values yield an unscaled discrete-valued pdf, which is integrated to create a cdf, and then linear interpolation is used to generate a continuous inverse cdf. I report the confidence limits such that the area in each tail is equal (green lines). But I then search systematically across values of the area in the left tail of the distribution (from 0 to alpha), finding the value that minimises the width of the 1-alpha confidence interval; the resulting confidence limits (red lines) are more satisfactory.

> f <- 18 ; n <- 20 # observed f successes out of n trials
> alpha <- 0.05
> 
> m = 10^5
> p=seq(0.5,1.0,1/m) # uniform prior
> pdf=dbinom(f,n,p) # not rescaled
> cdf=cumsum(pdf)  # "integration"
> cdf=cdf/cdf[1+m/2] # so now runs to 1
> invcdf <- approxfun(cdf,p) # function relies on linear interpolation
> scl = c(invcdf(alpha/2),invcdf(1-alpha/2)); scl # CLs with equal area in each tail
[1] 0.6964185 0.9695073
> 
>  mm = 10^5  # this section minimises width of CI
>  lt = seq(0,alpha,1/mm)  # area in left tail (0 to alpha in steps of 1/m)
>  i = which.min(invcdf(1-alpha+lt)-invcdf(lt))
>  i/(mm*alpha)  # ~0 => 1-tailed; ~0.5 => symmetric
[1] 0.8854
>  cl = c(invcdf(lt[i]),invcdf(1-alpha+lt[i])); cl # CLs minimising width of CI
[1] 0.7235043 0.9823723
> 
> plot(p,pdf,type="l", yaxt="n")
> abline(v=max(0.5,f/n),col="blue",lwd=4,lty=2) # observed
> abline(v=scl, col="green", lwd=1)  
> abline(v=cl, col="red", lwd=2)

pdf with limits

hutch
  • 61
  • 3