I have a normal random variable $X$ with mean $\mu$ and variance $\sigma^2$. Any advice on how to compute the conditional expectation $E[\frac{1}{X}|X \leq T]$ where $T$ is a positive constant?
Asked
Active
Viewed 66 times
0
-
1this link looks relevant. https://stats.stackexchange.com/questions/70045/mean-and-variance-of-inverse-of-a-normal-rv – mlofton Aug 14 '19 at 04:56
-
2As with the link above, the expectation will not converge, given the 1/X and the domain of support including 0. – wolfies Aug 14 '19 at 06:52
-
Because this conditional variable has positive continuous density in a neighborhood of zero, https://stats.stackexchange.com/questions/299722 demonstrates the expectation does not exist. – whuber Aug 14 '19 at 13:02
-
@whuber Yes, I saw some of those links before, but if the mean is sufficiently large, would that make it okay? Would simulation be the best way to approximate this? – dotpixel Aug 14 '19 at 16:49
-
No, it doesn't help. My analysis (in one of those answers) shows the result has nothing to do with the mean. It's all about the fact that there's sufficient probability for $X$ to be close enough to zero that no expectation can exist. This will be true of any Normal distribution (although, to be sure, as a *practical* matter that probability may be negligible: but that's a different question). – whuber Aug 14 '19 at 18:57
1 Answers
0
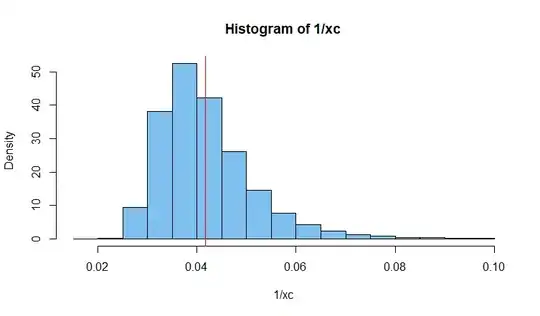
Comment: Simulation for $T = 10,$ which avoids taking reciprocals of values anywhere near $0.$ Then $E(\frac 1 X\, |\, X > 10) \approx 0.042.$ (As @Wolfies comments, this is a different problem.)
set.seed(2019)
x = rnorm(10^6, 25, 5)
xc = x[x > 10]
length(xc)
[1] 998638
a = mean(1/xc); a
[1] 0.04174508
hist(1/xc, prob=T, col="skyblue2")
abline(v=a, col="red")
Tangentially related application: Here
BruceET
- 47,896
- 2
- 28
- 76
-
2$X>T$ (for T positive) is not the same as $X < T$, when considering $\frac1X$ – wolfies Aug 14 '19 at 07:07
-
Right: Should have noted explicitly that I was changing the rules to get an expectation that exists. Editing. – BruceET Aug 14 '19 at 07:16