1

Wikipedia defines the weighted harmonic mean of a set of rates as follows:

$$H=\frac{\sum\limits_{i=1}^n w_i}{\sum\limits_{i=1}^n\frac{w_i}{x_i}}=\left(\frac{\sum\limits_{i=1}^n w_ix_i^{-1}}{\sum\limits_{i=1}^n w_i}\right)^{-1}$$

It then proceeds to give examples using rates expressed in terms of km/h. if the rates of which i want to calculate the harmonic mean are decimals less than 1 (as in rates of precision or recall), and i wish to arbitrarily weigh some of the rates as more important than others, what constraints if any must govern which weights i select? do they need to be decimals and sum to one?

Thanks!

voncat
  • 11
  • 2
  • The only circumstances in which this formula is undefined are when any division by zero is attempted; *viz.* (a) $\sum w_i=0$, (b) any $x_i=0,$ or (c) $\sum w_i x_i^{-1}=0.$ In your case (a) doesn't hold and (b) or (c) can hold only when at least one $x_i$ is zero. Thus, the answer depends on whether by "between 0 and 1" can possibly include $0$ or not. Which does it mean? – whuber Aug 12 '19 at 19:59
  • Sorry -- definitely does not include 0. edited to clarify. – voncat Aug 12 '19 at 20:06
  • Okay, thank you. Please explain what it means to "matter": since there is no mathematical issue to decide, what is your intended meaning of this? Is there some possibility that it makes no sense to compute a mean for the quantities represented by your decimals? If so, what kinds of quantities would those be? – whuber Aug 12 '19 at 20:07
  • @whuber i clarified my question -- asking about constraints on possible value of weights. thanks! – voncat Aug 13 '19 at 02:28
  • It's unclear what you mean by "decimals." The weights have to be nonnegative, as is almost always the case in any weighted average. The result is unchanged when you multiply them all by the same positive number--it just cancels in the fraction--so the sum-to-unity restriction is without meaning. – whuber Aug 13 '19 at 13:06
  • @whuber Figured it out, it was a PEMDAS issue. Thank you so much for all your help. – voncat Aug 13 '19 at 18:41

1 Answers1

1

Here is an example that might provide helpful intuition. In the US, automobile fuel efficiency is expressed in 'miles per (US) gallon' (mpg). with higher numbers indicating greater efficiency.

Harmonic mean for summarizing MPG. Suppose I take a weekend trip to mountains 100 miles away. Going uphill my car gets 15mpg and returning it gets 25mpg. That doesn't mean my average fuel efficiency for the trip is 20mpg. I used a total of $\frac{100}{15} + \frac{100}{25} = 10.67$ gallons to go $200$ miles, so the overall fuel efficiency is $200/10.67 = 18.74$mpg. Notice that this is a harmonic mean.

Arithmetic mean for summarizing metric efficiency data. Most of the rest of the world uses metric units in which fuel efficiency is often measured as the number of liters of fuel required to go 100km, so that lower numbers indicate better fuel efficiency. In metric, units my fuel efficiency is 15.68 going uphill and 9.41 going downhill, and the overall efficiency is just the (arithmetic) average 12.58 of these two numbers.

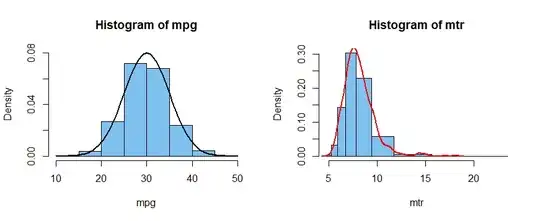
Distributions. Suppose the 1000 cars in a small US car rental company have fuel efficiencies distributed approximately $\mathsf{Norm}(\mu = 30, \sigma = 5)$ mpg. Then the metric fuel efficiencies could not be normal, but considerably right-skewed. (This may be reasonable because stopped, waiting for a green light, my instantaneous metric fuel efficiency is infinite.)

The histograms below show the US and metric fuel efficiencies of this hypothetical fleet of rental cars. Histogram bins for mpg in the left panel are of equal width. The density curve of $\mathsf{Norm}(30, 5)$ is shown.

In the panel at right, the bins are of unequal widths. They correspond to the bins at left, but in reverse order. A kernel density estimator of the transformed values is shown. (Transformation: mtr = 235.2/mpg.)

enter image description here

BruceET
  • 47,896
  • 2
  • 28
  • 76