Extrapolation v. Interpolation

Question

What is the difference between extrapolation and interpolation, and what is the most precise way of using these terms?

For example, I have seen a statement in a paper using interpolation as:

"The procedure interpolates the shape of the estimated function between the bin points"

A sentence that uses both extrapolation and interpolation is, for example:

The previous step where we extrapolated the interpolated function using the Kernel method to the left and right temperature tails.

Can someone provide a clear and easy way to distinguish them and guide how to use these terms correctly with an example?

[A related question.](https://stats.stackexchange.com/questions/219579) — J. M. is not a statistician, Jul 25 '19 at 07:18
Possible duplicate of [What is wrong with extrapolation?](https://stats.stackexchange.com/questions/219579/what-is-wrong-with-extrapolation) — usεr11852, Jul 25 '19 at 08:21
@usεr11852 I think the two questions cover similar ground but are different because this one asks for the contrast with interpolation. — mkt, Jul 25 '19 at 11:55
Has this distinction between interpolation and extrapolation been formalized rigorously in a generally agreed upon way, (e.g., via convex hulls) or are these terms still subject to human judgement and interpretation? — Nick Alger, Jul 25 '19 at 16:19

mkt · Accepted Answer · 2019-08-02T09:51:30.757

52

To add a visual explanation to this: let's consider a few points that you plan to model.

They look like they could be described well with a straight line, so you fit a linear regression to them:

This regression line lets you both interpolate (generate expected values in between your data points) and extrapolate (generate expected values outside the range of your data points). I've highlighted the extrapolation in red and the biggest region of interpolation in blue. To be clear, even the tiny regions between the points are interpolated, but I'm only highlighting the big one here.

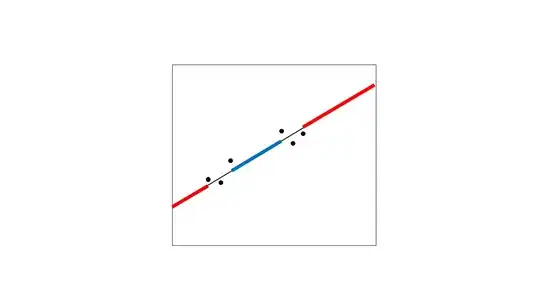
Why is extrapolation generally more of a concern? Because you're usually much less certain about the shape of the relationship outside the range of your data. Consider what might happen when you collect a few more data points (hollow circles):

It turns out that the relationship was not captured well with your hypothesized relationship after all. The predictions in the extrapolated region are way off. Even if you had guessed the precise function that describes this nonlinear relationship correctly, your data did not extend over enough of a range for you to capture the nonlinearity well, so you may still have been pretty far off. Note that this is a problem not just for linear regression, but for any relationship at all - this is why extrapolation is considered dangerous.

Predictions in the interpolated region are also incorrect because of the lack of nonlinearity in the fit, but their prediction error is much lower. There's no guarantee that you won't have an unexpected relationship in between your points (i.e. the region of interpolation), but it's generally less likely.

I will add that extrapolation is not always a terrible idea - if you extrapolate a tiny bit outside the range of your data, you're probably not going to be very wrong (though it is possible!). Ancients who had no good scientific model of the world would not have been far wrong if they forecast that the sun would rise again the next day and the day after that (though one day far into the future, even this will fail).

And sometimes, extrapolation can even be informative - for example, simple short-term extrapolations of the exponential increase in atmospheric CO$_2$ have been reasonably accurate over the past few decades. If you were a student who didn't have scientific expertise but wanted a rough, short-term forecast, this would have given you fairly reasonable results. But the farther away from your data you extrapolate, the more likely your prediction is likely to fail, and fail disastrously, as described very nicely in this great thread: What is wrong with extrapolation? (thanks to @J.M.isnotastatistician for reminding me of that).

Edit based on comments: whether interpolating or extrapolating, it's always best to have some theory to ground expectations. If theory-free modelling must be done, the risk from interpolation is usually less than that from extrapolation. That said, as the gap between data points increases in magnitude, interpolation also becomes more and more fraught with risk.

edited Aug 02 '19 at 09:51

answered Jul 23 '19 at 15:42

mkt

11,770
9
51
125

5

I like your answer, and regard it as complementary to mine and in no sense competing. But a small point, important for some readers, is that red and green are hard for quite a few people to distinguish visually. – Nick Cox Jul 24 '19 at 10:27
1

@NickCox Good point, thank you for raising that - I've now changed the colour scheme. – mkt Jul 24 '19 at 11:06
I don't like this answer very much. The fact that your example data is just two blobs means (or at least it _could mean_; it's hard to be confident with only six sample points) that interpolating between them could also be considered extrapolating outside of the data support. And it would be quite conceivable for the extra data points to diverge strongly in that region. There might actually be a better quadratic model. If you're going to interpolate in such a situation, you'd better had an a-priori reason for preferring a particular model. And that is also the case for your CO₂ example! – leftaroundabout Jul 24 '19 at 14:28
@leftaroundabout The fact that the true shape is ambiguous in the example is intentional. But would it matter a great deal for the argument if the gap between the point groups was narrower? As I mention in the answer itself, interpolation can go wrong too - you're just less likely to encounter large changes in shape there. Regarding your claim that "*interpolating between them could also be considered extrapolating outside of the data support*", I think that is simply incorrect. The data range encompasses all the points, and no amount of clustering alters that. – mkt Jul 24 '19 at 14:59
@leftaroundabout I completely agree that there might be a better model for the data points I present - that was the point of the final figure. But even with a poor model, the interpolation performs better than extrapolation, which is not an uncommon occurrence, though not universal (which I note in the answer). – mkt Jul 24 '19 at 15:02
@leftaroundabout I don't understand your point about interpolation as it pertains to the CO2 example, since those measurements are so frequent that interpolation is uncontroversial: https://www.biointeractive.org/sites/default/files/styles/feature_image/public/Biointeractive/IOTW/keeling-onpg.jpg?itok=RIQUP1a8 – mkt Jul 24 '19 at 15:04
@mkt IMO it would matter if the gap were narrower. Namely, in this case you'd need to make a pretty contrived model to get interpolation that would diverge a lot from the simple linear or quadratic interpolation, whereas with two disconnected blobs, you could e.g. have a polynomial model and a sinusoidal models that have the same number of parameters, agree perfectly within each of the blobs, but diverge completely in the gap between the blobs. – leftaroundabout Jul 24 '19 at 15:05
Regarding the CO₂ example: sure, _now_ we have a great history of measurements between which we can interpolate. But your point (as I understand it; and I'd agree with it) is that we can _also_ reasonably extrapolate. But that has little to do with the density of data points, but with the fact that we have some a-priori ideas how the emissions will likely develop – as well as, more interestingly, how the climate would respond to that. These ideas come from basic physics, i.e. they are simple yet grand-scheme effective. That's why extrapolation is sensible in climate prediction. – leftaroundabout Jul 24 '19 at 15:09
1

@leftaroundabout My point was that the Keeling curve pattern is so strong that extrapolations ignoring economics & physics are still reasonably accurate on the scale of years to a few decades. I noted 'past few decades' precisely because that's the time scale on which we have had high-resolution measurements. This is an example where extrapolation would *not* have led you badly wrong and I think that's worth noting. I think it would take wilful misreading to claim that this answer is *advocating* theory-free extrapolation. – mkt Jul 24 '19 at 15:23
1

Relatedly, I gave Taleb's "turkey example" in [this answer](https://stats.stackexchange.com/a/219781) as a warning for people who use extrapolation. – J. M. is not a statistician Jul 25 '19 at 07:18
@J.M.isnotastatistician Thanks, that's a very nice example and a great thread that I had forgotten about. Will edit my answer to refer to it. – mkt Jul 25 '19 at 07:20
2

Extrapolation is especially problematic when you have overfitting; with a polynomial model, for instance, going significantly outside the data set will result in the highest order term blowing up. – Acccumulation Jul 25 '19 at 20:18

score 21 · Answer 2 · edited Jul 26 '19 at 11:24

21

In essence interpolation is an operation within the data support, or between existing known data points; extrapolation is beyond the data support. Otherwise put, the criterion is: where are the missing values?

One reason for the distinction is that extrapolation is usually more difficult to do well, and even dangerous, statistically if not practically. That is not always true: for example, river floods may overwhelm the means of measuring discharge or even stage (vertical level), tearing a hole in the measured record. In those circumstances, interpolation of discharge or stage is difficult too and being within the data support does not help much.

In the long run, qualitative change usually supersedes quantitative change. Around 1900 there was much concern that growth in horse-drawn traffic would swamp cities with mostly unwanted excrement. The exponential in excrement was superseded by the internal combustion engine and its different exponentials.

A trend is a trend is a trend,
But the question is, will it bend?
Will it alter its course
Through some unforeseen force
And come to a premature end?

-- Alexander Cairncross

Cairncross, A. 1969. Economic forecasting. The Economic Journal, 79: 797-812. doi:10.2307/2229792 (quotation on p.797)

edited Jul 26 '19 at 11:24

amoeba

93,463
28
275
317

answered Jul 23 '19 at 15:28

Nick Cox

48,377
8
110
156

1

Good answer. The interpretation is right there in the name - interpolation = to smooth within, extrapolation = to smooth beyond. – Nuclear Hoagie Jul 23 '19 at 15:33
1

IMO this is the correct answer. “Data support” is the crucial bit; even if the point you want to go is between two measured ones then it may still lie outside the data support. For example, if you have prosperity data for people in the Roman antiquity and from the modern day, but not in between, then interpolating into the middle ages would be very problematic. I'd call this extrapolation. OTOH, if you have data scattered sparsely but uniformly through the entire time span, then interpolating to a particular year is much more plausible. – leftaroundabout Jul 24 '19 at 14:35
1

@leftaroundabout Just because interpolation may be done over a huge gap in data does not make it extrapolation. You're mistaking the advisability of the procedure for the procedure itself. Sometimes interpolation is a bad idea too. – mkt Jul 24 '19 at 15:41
@mkt ok, different example: temperature measurements on the Earth surface. Say we have dense enough measurements all the way up to 70°N, but none further north. Now, is it extrapolation to estimate the temperature at the north pole? Is it extrapolation if we had measurements up to 89.9°N? – leftaroundabout Jul 24 '19 at 15:46
1

@mkt: I'm going to side with leftaroundabout that his first example *could* be considered extrapolation, as interpolation vs extrapolation isn't really as well defined as we may want to think. A simple transformation of variables can turn interpolation into extrapolation. In his example, using something like distance functions instead of raw time means that while in raw time we are interpolating, in distances we are extrapolating...and using raw times would probably be a bad idea. – Cliff AB Jul 24 '19 at 17:45
@CliffAB I don't think your transformation example changes my view. The range of the data - and consequently the terms interpolation and extrapolation - are defined with reference to an axis. If you change the axis, the reference frame has changed. So to my mind the two situations (interpolation on one axis and extrapolation on another) are easy to reconcile. – mkt Jul 25 '19 at 08:27
@mkt the concept of an “axis” doesn't really make sense in the general case (data on a manifold). I suppose you could mean “geodesic”. But already in a 2D Euclidean space, you generally won't have more than two points sitting on a straight line, so even _within_ the data support you would always need to call it extrapolation. That would make the term “interpolation” completely useless. – leftaroundabout Jul 25 '19 at 11:22
1

This is my answer. I don't feel the need to qualify it. A broad distinction between interpolation and extrapolation doesn't rule it out being a little difficult to decide which is being undertaken. If you have a big hole in the middle of the data space, labelling could go either way. As some wag pointed out, the fact that the end of the day and the beginning of the night blur into one another doesn't make the distinction between day and night pointless or useless. – Nick Cox Jul 25 '19 at 13:21
I know this is a basic principle, but is there a particular place I could look for further exploration of in-support vs. out-of-support prediction? Even just a pointer to a basic undergrad book chapter would be very appreciated. (But I would ideally love to see things like confidence bounds derivations, and discussion in terms of particular model classes, noise priors, true underlying distributions, etc.) – kdbanman Nov 13 '19 at 20:50
I don’t have a reference of that kind for you. Perhaps it exists in kriging or Gaussian process regression literatures – Nick Cox Nov 13 '19 at 21:31

score 13 · Answer 3 · answered Jul 24 '19 at 01:02

TL;DR version:

Interpolation takes place between existing data points.
Extrapolation takes place beyond them.

Mnemonic: interpolation => inside.

FWIW: The prefix inter- means between, and extra- means beyond. Think also of interstate highways which go between states, or extraterrestrials from beyond our planet.

score 1 · Answer 4 · edited Nov 14 '19 at 12:46

Example:

Study: Want to fit a simple linear regression on the height on the age for girls of age 6-15 years old. Sample size is 100, age is calculated by (date of measuring - date of birth)/365.25.

After data collection, model is fit and get the estimate of intercept b0 and slope b1. it means we have E(height|age) = b0 + b1*age.

When you want the mean height for age 13, you find that there is no 13 year old girl in your sample of 100 girls, one of them is 12.83 years old and one is 13.24.

Now you plug in age = 13 into formula E(height|age) = b0 + b1*age. It is called interpolation because 13 year old is covered by the range of your data used to fit model.

If you want to get mean height for age 30 and use that formula, that is called extrapolation, because age 30 is out of the range of the age covered by your data.

If the model has several covariates, you need to be careful because it is hard to draw the border that data covered.

In statistics, we do not advocate extrapolation.

"In statistics, we do not advocate extrapolation." A major fraction of time series analysis does precisely that.... — Nick Cox, Nov 14 '19 at 12:46

score 0 · Answer 5 · answered Oct 12 '20 at 13:32

The extrapolation v.s. interpolation also applys in neural networks as mentioned in Rethinking Eliminative Connectionism and Deep Learning: A Critical Appraisal:

generalization can be thought of as coming in two flavors, interpolation between known examples, and extrapolation, which requires going beyond a space of known training examples

The author wrote that extrapolation is a wall stopping us reaching artificial general intelligence.

Let's suppose that we train a translation model to translate English to German very well with tons of data, we can be sure that it can fail a test with randomly permutated English words because it has never seen such data in the training process and it is certain to fail a new phrase coined after it is trained. That is it behaves badly for open-ended inferences because it can be only accurat for data similar to the training ones but the real world is open-ended.

References:

Extrapolation v. Interpolation

5 Answers5

Linked