What is wrong with extrapolation?

Question

I remember sitting in stats courses as an undergrad hearing about why extrapolation was a bad idea. Furthermore, there are a variety of sources online which comment on this. There's also a mention of it here.

Can anyone help me understand why extrapolation is a bad idea? If it is, how is it that forecasting techniques aren't statistically invalid?

If you properly train a regression learner I can't see what's wrong. — Firebug, Jun 19 '16 at 16:41
@Firebug Mark Twain had something to say about that. The relevant passage is quoted near the end of my answer at http://stats.stackexchange.com/a/24649/919 . — whuber, Jun 20 '16 at 17:26
@whuber I guess that isn't exactly extrapolation thinking about it now. Say, we properly train and validate an algorithm to predict data one week into the feature. Doing the correct resampling (and tuning, if there are hyperparameters to be tuned), then I can't see what's wrong if that, you have a response and you should also know the confidence of that response. Now, if you train your algorithm in a week to week basis you can't expect to accurately predict one year into the future. Sorry for the possible confusion. — Firebug, Jun 20 '16 at 17:55
@Firebug No need to apologize--your remarks contain useful clarifying information. As I read them, they suggest "extrapolate" can have multiple interpretations in a forecasting setting. One is that it involves an "extrapolation" of time. But when you look at standard time-series models, *especially those where time is not an explicit covariate,* they predict future values *in terms of previous values*. When those previous values remain within the ranges of past previous values, *the model performs no extrapolation at all!* Therein may lie a resolution of the apparent paradox. — whuber, Jun 20 '16 at 18:25
@whuber Yes, that makes a lot of sense. It's still interpolation, just between a time period and the next one. What I had in mind were last words in the question: _"If it is, how is it that forecasting techniques aren't statistically invalid?"_, which would make no practical sense, eg. banks worldwide invest millions on forecasting, no one invest millions in something that doesn't work. — Firebug, Jun 20 '16 at 18:31
Interpolation could be as bad as interpolation. For instance, if there's a singularity in the range of your observations, but your fit function doesn't account for it, you're going to miss the singularity. — Aksakal, Jun 20 '16 at 18:33
I'm no statistician, but it seems to me (from real-world software dev experience) that how far the prediction extends needs to be limited by how inaccurate the data is— closer-fitting data would allow long extrapolation, and loose-fitting short extrapolation allowance. Or, the extrapolation should be modeled as a range of values (area?) with the breadth of plausible extrapolated values proportional to less-accurate/looser-fitting data points. This would prevent the grossly inaccurate predictions in Kostia's & Laurent Duval's answer's graphs. — Slipp D. Thompson, Jun 23 '16 at 07:02
I'm also curious why all the answers assume linear functions for extrapolation? _Again from my real-world software development experience_, I've found straight-line extrapolation to be mostly useless, even when using generated data (vs. sampled data); a 2nd-degree-or-higher polynomial function is usually necessary for any kind of accuracy, for even a single render pass ahead of present. I suppose you could data-fit to polynomials; I've only analyzed 1st & 2nd derivates of current vs. previous samples to predict future values with 3rd-degree-polynomial-type curvature. — Slipp D. Thompson, Jun 23 '16 at 07:16
@SlippD.Thompson In the second xkcd comic, the extrapolation is log-linear, and it's still terrible. — noɥʇʎԀʎzɐɹƆ, Jun 25 '16 at 20:12
@uoɥʇʎPʎzɐɹC True. But it's still an arbitrary curve thrown on top of data. To accurately extrapolate NGram data, I would think a function would need to be derived from all word growth ever; especially words that have already reached and fallen from a saturation point. I imagine that the func would be a product of both time & frequency at past time(s). Really, any extrapolation function needs to be able to predict past data using further-past data with reasonable accuracy in order to be considered; log-linear would never pass this test over for NGrams that have risen then flattened or fallen. — Slipp D. Thompson, Jun 25 '16 at 20:30
@SlippD.Thompson see the turkey parable linked to from my answer; imagine if the data was about the global economy before the 1930s; also more data ≠ more accuracy, see the first comic - any extrapolation function would predict a > 1 # of husbands — noɥʇʎԀʎzɐɹƆ, Jun 27 '16 at 19:55
@SlippD.Thompson Actually, I was able to explain that with another xkcd comic in my updated answer — noɥʇʎԀʎzɐɹƆ, Jun 27 '16 at 20:02
see http://stats.stackexchange.com/questions/221379/what-are-the-theoretical-reasons-for-why-extrapolation-less-reliable-than-inte/221398#221398 — , Jun 30 '16 at 08:00
Too many people say extrapolation is **wrong**, **Don't take assumptions**. Pleas ensure that if you say it's bad, so what is better? ` With no better idea, each one claims that its bad` Are we playing memes and those who have better ones win?? What if its totally wrong? If you don't have any other option. For example, we have data of the times that 25-35 y-o male people have run a 1-mile tract, and we want to see how a 75 y-o will do it. if we `estimate` it by linear regression, we are being naive, for sure. But please give a better idea. This is not a game to win battle by mocking a suitable — Sadegh, Jun 10 '21 at 12:30

score 103 · Answer 1 · edited Jun 20 '16 at 13:56

103

A regression model is often used for extrapolation, i.e. predicting the response to an input which lies outside of the range of the values of the predictor variable used to fit the model. The danger associated with extrapolation is illustrated in the following figure.

The regression model is “by construction” an interpolation model, and should not be used for extrapolation, unless this is properly justified.

edited Jun 20 '16 at 13:56

psmears

131
3

answered Jun 19 '16 at 06:31

Kostia

1,567
1
8
9

1

This is a *terrible* example against extrapolation. The straight regression line fit data points much better than your curvy true function. – horaceT Jun 22 '16 at 05:17
15

"The straight regression line fit data points much better than your curvy true function" This statement is false. The RSS for the true regression function is smaller than RSS for the simple regression line, – Kostia Jun 22 '16 at 07:26
Point taken and you may (should) be right. But judging from the batch of points, there is no way one could infer the true function. – horaceT Jun 22 '16 at 16:20
39

Exactly. And this why extrapolation may be a bad idea. – Kostia Jun 22 '16 at 16:27
"The regression model is “by construction” an interpolation model" -> I guess we can have exactly the same issue with interpolation (even if it's less likely to happen) – Metariat Jun 28 '16 at 16:04
see http://stats.stackexchange.com/questions/221379/what-are-the-theoretical-reasons-for-why-extrapolation-less-reliable-than-inte/221398#221398 – Jun 30 '16 at 08:01
@Kostia I might disagree that regression models (with time as a covariate) are often used for extrapolation or that if they are, those rogue analysts are going against the general consensus of statistics. ARIMA models are employed with adequate success and conservatism in most areas of research. – AdamO Dec 29 '17 at 22:50

score 94 · Answer 2 · edited Apr 13 '17 at 12:44

94

This xkcd comic explains it all.

Using the data points Cueball (the man with the stick) has, he has extrapolated that the woman will have "four dozen" husbands by late next month, and used this extrapolation to lead to the conclusion of buying the wedding cake in bulk.

Edit 3: For those of you who say "he doesn't have enough data points", here's another xkcd comic:

Here, the usage of the word "sustainable" over time is shown on a semi-log plot, and extrapolating the data points we receive an unreasonable estimates of how often the word "sustainable" will occur in the future.

Edit 2: For those of you who say "you need all past data points too", yet another xkcd comic:

Here, we have all past data points but we fail to accurately predict the resolution of Google Earth. Note that this is a semi-log graph too.

Edit: Sometimes, even the strongest of (r=.9979 in this case) correlations are just plain wrong.

If you extrapolate without other supporting evidence you also violating correlation does not imply causation; another great sin in the world of statistics.

If you do extrapolate X with Y, however, you must make sure that you can accurately (enough to satisfy your requirements) predict X with only Y. Almost always, there are multiple factors than impact X.

_{I would like to share a link to another answer that explains it in the words of Nassim Nicholas Taleb.}

edited Apr 13 '17 at 12:44

Community

1

answered Jun 19 '16 at 19:48

noɥʇʎԀʎzɐɹƆ

891
5
11

17

xkcd has a joke about every possible maths/statistics problem one may encounter, doesn't it? – Ander Biguri Jun 20 '16 at 17:10
@AnderBiguri yep. :) – noɥʇʎԀʎzɐɹƆ Jun 20 '16 at 17:11
26

This idea might as well be used as an argument against interpolating: "last night you had 0.5 husbands". – JiK Jun 21 '16 at 12:15
3

@JiK If all you know is that she has one now, and two days ago she had none, that is not a bad estimate ;-) – Dennis Jaheruddin Jun 22 '16 at 08:42
9

Sustainable sustainable Sustainable sustainable sustainable sustainable Sustainable sustainable. https://en.wikipedia.org/wiki/Buffalo_buffalo_Buffalo_buffalo_buffalo_buffalo_Buffalo_buffalo – Meni Rosenfeld Jun 22 '16 at 11:41
1

An answer constructed (almost) entirely of XKCD comics?! Brilliant! – BarocliniCplusplus Feb 05 '21 at 21:42

Laurent Duval · Answer 3 · 2020-10-12T21:19:29.640

"Prediction is very difficult, especially if it's about the future". The quote is attributed to many people in some form. I restrict in the following "extrapolation" to "prediction outside the known range", and in a one-dimensional setting, extrapolation from a known past to an unknown future.

So what is wrong with extrapolation. First, it is not easy to model the past. Second, it is hard to know whether a model from the past can be used for the future. Behind both assertions dwell deep questions about causality or ergodicity, sufficiency of explanatory variables, etc. that are quite case dependent. What is wrong is that it is difficult to choose an single extrapolation scheme that works fine in different contexts, without a lot of extra information.

This generic mismatch is clearly illustrated in the Anscombe quartet dataset shown below. The linear regression is also (outside the $x$-coordinate range) an instance of extrapolation. The same line regresses four set of points, with the same standard statistics. However, the underlying models are quite different: the first one is quite standard. The second is a parametric model error (a second or third degree polynomial could be better suited), the third shows a perfect fit except for one value (outlier?), the fourth a lack of smooth relationships (hysteresis?).

However, forecasting can be rectified to some extend. Adding to other answers, a couple of ingredients can help practical extrapolation:

You can weight the samples according to their distance (index $n$) to the location $p$ where you want to extrapolate. For instance, use an increasing function $f_p(n)$ (with $p\ge n$), like exponential weighting or smoothing, or sliding windows of samples, to give less importance to older values.
You can use several extrapolation models, and combine them or select the best (Combining forecasts, J. Scott Armstrong, 2001). Recently, there have been a number of works on their optimal combination (I may provide references if needed).

Recently, I have been involved in a project for extrapolating values for the communication of simulation subsystems in a real-time environment. The dogma in this domain was that extrapolation may cause instability. We actually realized that combining the two above ingredients was very efficient, without noticeable instability (without a formal proof yet: CHOPtrey: contextual online polynomial extrapolation for enhanced multi-core co-simulation of complex systems, Simulation, 2017). And the extrapolation worked with simple polynomials, with a very low computational burden, most of the operations being computed beforehand and stored in look-up tables.

Finally, as extrapolation suggests funny drawings, the following is the backward effect of linear regression:

+1 Nice answer. According to [this website](http://quoteinvestigator.com/2013/10/20/no-predict/) it seems unlikely that Bohr said it. It seems more likely to be an uncommon but generic Danish proverb. — usεr11852, Jun 19 '16 at 20:12
@usεr11852 Unlikely he "ever said that"? That why I said "attributed", should I be more cautious? — Laurent Duval, Jun 19 '16 at 20:21
I never said the *ever* part. I made this comment because given that the saying seems much more likely to be a Danish proverb, attributing it to a particular (extremely emblematic) Dane seems a bit of over-billing - especially given that there are no records of Bohr saying it. The original author might be an unnamed fisherman commenting on tomorrow's catch! I am rooting for the little guy here! :D — usεr11852, Jun 19 '16 at 20:35
This answer appears to equate extrapolation with *prediction*--but the two are not necessarily the same. In fact, incorrectly equating the two concepts may be the source of the paradox expressed in the question. — whuber, Jun 20 '16 at 18:27
@whuber forecasting and extrapolation are used in the question. I indeed used predictions. I restricted here extrapolation as "prediction out of the range". Wrong? Suggestions? — Laurent Duval, Jun 20 '16 at 19:11
Certainly the question uses both words: the entire point is whether "forecasting" has to be considered a form of "extrapolation." According to your introductory comments, you seem to define extrapolation as using the past to "model the future." Until you offer clear and distinct definitions of each, your answer could be misunderstood. — whuber, Jun 20 '16 at 19:54

usεr11852 · Answer 4 · 2016-06-19T08:30:05.757

Although the fit of a model might be "good", extrapolation beyond the range of the data must be treated skeptically. The reason is that in many cases extrapolation (unfortunately and unavoidably) relies on untestable assumptions about the behaviour of the data beyond their observed support.

When extrapolating one must do two judgement calls: First, from a quantitative perspective, how valid is the model outside the range of the data? Second, from a qualitative perspective, how plausible is a point $x_{out}$ laying outside the observed sample range to be a member of the population we assume for the sample? Because both questions entail a certain degree of ambiguity extrapolation is considered an ambiguous technique too. If you have reasons to accept that these assumptions hold, then extrapolation is usually a valid inferential procedure.

An additional caveat is that many non-parametric estimation techniques do not permit extrapolation natively. This problem is particularly noticeable in the case of spline smoothing where there are no more knots to anchor the fitted spline.

Let me stress that extrapolation is far from evil. For example, numerical methods widely used in Statistics (for example Aitken's delta-squared process and Richardson's Extrapolation) are essentially extrapolation schemes based on the idea that the underlying behaviour of the function analysed for the observed data remains stable across the function's support.

Altho it is possible to write safeguards for Wynn $\varepsilon$ (the computationally useful generalization of Aitken $\Delta^2$) and Richardson extrapolation, it can and does happen that the assumptions underlying these algorithms are not very well satisfied by sequences fed to it. When using these extrapolation methods with sequences of uncertain provenance, the sufficiently paranoid will usually have two or more of these convergence acceleration methods at hand for testing, and will only trust the results if at least two of these conceptually very different methods agree in their results. — J. M. is not a statistician, Jun 23 '16 at 04:26

Tim · Answer 5 · 2020-07-02T08:28:53.747

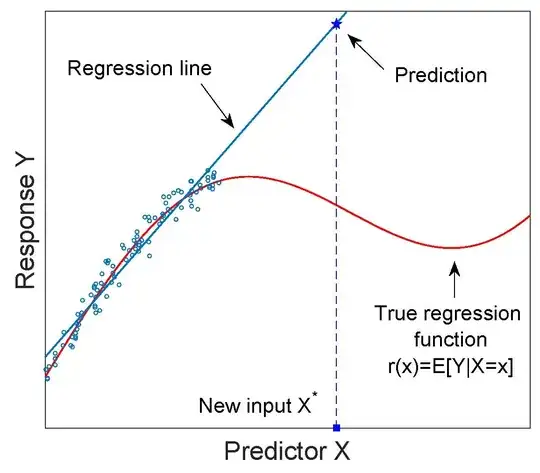
Contrary to other answers, I'd say that there is nothing wrong with extrapolation as far as it is not used in mindless way. First, notice that extrapolation is:

the process of estimating, beyond the original observation range, the value of a variable on the basis of its relationship with another variable.

...so it's very broad term and many different methods ranging from simple linear extrapolation, to linear regression, polynomial regression, or even some advanced time-series forecasting methods fit such definition. In fact, extrapolation, prediction and forecast are closely related. In statistics we often make predictions and forecasts. This is also what the link you refer to says:

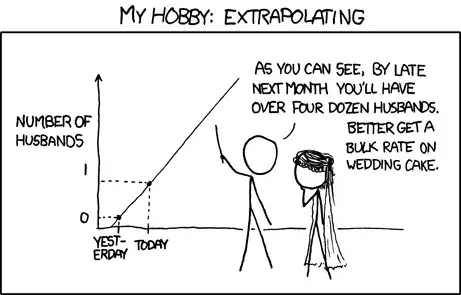
We’re taught from day 1 of statistics that extrapolation is a big no-no, but that’s exactly what forecasting is.

Many extrapolation methods are used for making predictions, moreover, often some simple methods work pretty well with small samples, so can be preferred then the complicated ones. The problem is, as noticed in other answers, when you use extrapolation method improperly.

For example, many studies show that the age of sexual initiation decreases over time in western countries. Take a look at a plot below about age of first intercourse in the US. If we blindly used linear regression to predict age of first intercourse we would predict it to go below zero at some number of years (accordingly with first marriage and first birth happening at some time after death)... However, if you needed to make one-year-ahead forecast, then I'd guess that linear regression would lead to pretty accurate short term predictions for the trend.

(source guttmacher.org)

Another great example comes from completely different domain, since it is about "extrapolating" for test done by Microsoft Excel, as shown below (I don't know if this is already fixed or not). I don't know the author of this image, it comes from Giphy.

All models are wrong, extrapolation is also wrong, since it wouldn't enable you to make precise predictions. As other mathematical/statistical tools it will enable you to make approximate predictions. The extent of how accurate they will be depends on quality of the data that you have, using methods adequate for your problem, the assumptions you made while defining your model and many other factors. But this doesn't mean that we can't use such methods. We can, but we need to remember about their limitations and should assess their quality for a given problem.

When the data you use for regression ends in the early 1980s, you can probably easily test how long beyond that date extrapolation would work. — gerrit, Jun 20 '16 at 10:35
@gerrit I agree, but unfortunately I wasn't able to find appropriate data. But if someone could point it to me then I'd be happy to update my answer for such comparison. — Tim, Jun 27 '16 at 10:05
In this case, the extrapolation fails, given that the age of first sex has jumped in the past several years. (But data for this always lags birth year by a couple of decades, for reasons that should be obvious.) — David Manheim, Oct 01 '17 at 18:38

score 15 · Answer 6 · edited Apr 13 '17 at 12:58

15

I quite like the example by Nassim Taleb (which was an adaptation of an earlier example by Bertrand Russell):

Consider a turkey that is fed every day. Every single feeding will firm up the bird's belief that it is the general rule of life to be fed every day by friendly members of the human race "looking out for its best interests," as a politician would say. On the afternoon of the Wednesday before Thanksgiving, something unexpected will happen to the turkey. It will incur a revision of belief.

Some mathematical analogs are the following:

knowledge of the first few Taylor coefficients of a function does not always guarantee that the succeeding coefficients will follow your presumed pattern.
knowledge of a differential equation's initial conditions does not always guarantee knowledge of its asymptotic behavior (e.g. Lorenz's equations, sometimes distorted into the so-called "butterfly effect")

Here is a nice MO thread on the matter.

edited Apr 13 '17 at 12:58

Community

1

answered Jun 20 '16 at 13:23

J. M. is not a statistician

1,785
1
15
23

3

…and of course, Taleb has to point out the moral lesson: **"don't be a turkey"!** In this context: don't be a careless extrapolator, and don't succumb to the sin of hubris. – J. M. is not a statistician Jun 25 '16 at 21:59
@uoɥʇʎPʎzɐɹC, I wasn't asking for it, but thank you! – J. M. is not a statistician Jul 31 '16 at 17:22
don't really have a use for cross validated reputation - and nobody saw your answer and it was really good. Enjoy! – noɥʇʎԀʎzɐɹƆ Jul 31 '16 at 17:23

einpoklum · Answer 7 · 2019-05-17T10:04:36.127

12

Ponder the following story, if you will.

I also remember sitting in a Statistics course, and the professor told us extrapolation was a bad idea. Then during the next class he told us it was a bad idea again; in fact, he said it twice.

I was sick for the rest of the semester, but I was certain I couldn't have missed a lot of material, because by the last week the guy must surely have been doing nothing but telling people again and again how extrapolation was a bad idea.

Strangely enough, I didn't score very high on the exam.

edited May 17 '19 at 10:04

answered Jun 19 '16 at 11:42

einpoklum

300
1
9

6

The question asks "what is wrong with extrapolation?". We are looking for answers that give reasons why extrapolation could be a bad idea. – Robert Long Jun 19 '16 at 11:52
8

@RobertLong: It's actually a kind of meta/joke answer, and pretty similar to https://xkcd.com/605/ - still maybe better as a comment than an answer though. – Neil Slater Jun 19 '16 at 19:44
@NeilSlater: You should have posted your comment as an answer... :) – usεr11852 Jun 19 '16 at 20:15
@RobertLong: This is that kind of answer. It simply has the form of a parable. – einpoklum Jun 19 '16 at 23:24
@NeilSlater: My answer is pretty close to Kostia's, except that his model function is linear and mine was exponential (and he had more samples like a good statistician, unlike myself, the slacker first-year student. – einpoklum Jun 19 '16 at 23:29
@einpoklum OK , sorry. haha I got it, +1 – Robert Long Jun 19 '16 at 23:32
2

It is not clear that your model is exponential. – gerrit Jun 20 '16 at 10:37

score 7 · Answer 8 · answered Jun 22 '16 at 13:58

The question is not just statistical, it's also epistemological. Extrapolation is one of the ways we learn about the nature, it's a form of induction. Let's say we have data for electrical conductivity of a material in a range of temperatures from 0 to 20 Celsius, what can we say about the conductivity at 40 degree Celsius?

It's closely related to small sample inference: what can we say about the entire population from measurements conducted on a small sample? This was started by Gosset as Guiness, who came up with Student t-distributions. Before him statisticians didn't bother to think about small samples assuming that the sample size can always be large. He was at Guinnes and had to deal with samples of beer to decide what to do with the entire batch of beer to ship.

So, in practice (business), engineering and science we always have to extrapolate in some ways. It could be extrapolating small samples to large one, or from limited range of input conditions to a wider set of conditions, from what's going on in the accelerator to what happened to a black hole billions of miles away etc. It's especially important in science though, as we really learn by studying the discrepancies between our extrapolation estimates and actual measurements. Often we find new phenomena when the discrepancies are large or consistent.

hence, I say there is no problem with extrapolation. It's something we have to do every day. It's just difficult.

score 4 · Answer 9 · answered Jun 20 '16 at 02:36

Extrapolation itself isn't necessarily evil, but it is a process which lends itself to conclusions which are more unreasonable than you arrive at with interpolation.

Extrapolation is often done to explore values quite far from the sampled region. If I'm sampling 100 values from 0-10, and then extrapolate out just a little bit, merely to 11, my new point is likely 10 times further away from any datapoint than any interpolation could ever get. This means that there's that much more space for a variable to get out of hand (qualitatively). Note that I intentionally chose only a minor extrapolation. It can get far worse
Extrapolation must be done with curve fits that were intended to do extrapolation. For example, many polynomial fits are very poor for extrapolation because terms which behave well over the sampled range can explode once you leave it. Good extrapolation depends on a "good guess" as to what happens outside of the sampled region. Which brings me to...
It is often extremely difficult to use extrapolation due to the presence of phase transitions. Many processes which one may wish to extrapolate on have decidedly nonlinear properties which are not sufficiently exposed over the sampled region. Aeronautics around the speed of sound are an excellent example. Many extrapolations from lower speeds fall apart as you reach and exceed the speed of information transfer in the air. This also occurs quite often with soft sciences, where the policy itself can impact the success of the policy. Keynesian economics extrapolated out how the economy would behave with different levels of inflation, and predicted the best possible outcome. Unfortunately, there were second order effects and the result was not economic prosperity, but rather some of the highest inflation rates the US has seen.
People like extrapolations. Generally speaking, people really want someone to peer into a crystal ball and tell them the future. They will accept surprisingly bad extrapolations simply because it's all the information they have. This may not make extrapolation itself bad, per se, but it is definitely something one should account for when using it.

For the ultimate in extrapolation, consider the Manhattan Project. The physicists there where forced to work with extremely small scale tests before constructing the real thing. They simply didn't have enough Uranium to waste on tests. They did the best they could, and they were smart. However, when the final test occurred, it was decided that each scientist would decide how far away from the blast they wanted to be when it went off. There was substantial differences of opinion as to how far away was "safe" because every scientists knew they were extrapolating quite far from their tests. There was even a non-trivial consideration that they might set the atmosphere on fire with the nuclear bomb, an issue also put to rest with substantial extrapolation!

score 3 · Answer 10 · answered Jul 26 '16 at 03:51

Lots of good answers here, I just want to try and synthesize what I see as the core of the issue: it is dangerous to extrapolate beyond that data generating process that gave rise to the estimation sample. This is sometimes called a 'structural change'.

Forecasting comes with assumptions, the main one being that the data generating process is (as near as makes no significant difference) the same as the one that generated the sample (except for the rhs variables, whose changes you explicitly account for in the model). If a structural change occurs (i.e. Thanksgiving in Taleb's example), all bets are off.

What is wrong with extrapolation?

10 Answers10

Linked