I am trying to understand the mathematics underneath the poisson.test function in the stats package in R. I am using it to compute a p-value when comparing a sample of data against another poisson rate; not another sample of data.
I've looked up the documentation around this but I cannot find anything which outlines the mathematics of the test itself, only how it is used. If anyone is able to help, or point me in the right direction I'd be greatly appreciative.
When you say "another Poisson rate" ... if that other Poisson rate is derived from data then you are comparing data with data.
I'll assume you mean against some prespecified/theoretical rate (i.e. that you're performing a one-sample test).
You didn't state whether you were doing a one-tailed or two-tailed test. I'll discuss both
What it's doing is using the Poisson distribution with the specified rate you're testing against, and then computing the tail area "at least as extreme" (in the direction of the alternative) as the sample you got.
e.g. consider a one-tailed test; $H_0: \mu \leq 8.5$ vs $H_1: \mu > 8.5$ and the observed Poisson count of 14. Then we can compute that the upper tail at and above 14 has 0.0514 of the probability - e.g.:
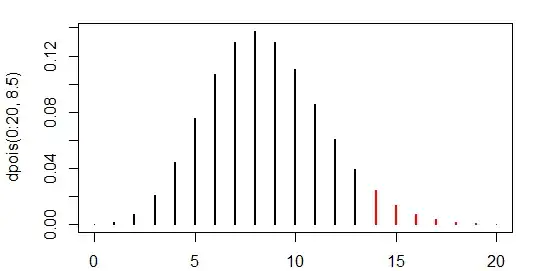
> 1-ppois(13,8.5)
[1] 0.05141111
(I realize this is not the best way to compute this in R - we should use the lower.tail argument instead - but wanted to make it more transparent to readers less familiar with R; by comparison ppois(13,8.5,lower.tail=FALSE) looks like an off-by-one error)
This calculation agrees with poisson.test:
> poisson.test(14,r=8.5,alt="greater")
Exact Poisson test
data: 14 time base: 1
number of events = 14, time base = 1, p-value = 0.05141
alternative hypothesis: true event rate is greater than 8.5
95 percent confidence interval:
8.463938 Inf
sample estimates:
event rate
14
With a two-tailed test it sums those values with equal or lower probability (i.e. as with typical Fisher-style exact tests, it uses the likelihood under the null to identify what's "more extreme"):
The probability of a 14 with Poisson mean 8.5 is about 0.024 and in the left tail the largest x-value with probability no larger occurs at 3, so the probabilities of 0,1,2 and 3 are added in:
> 1-ppois(13,8.5)+ppois(3,8.5)
[1] 0.08152019
check against the output:
> poisson.test(14,r=8.5)
Exact Poisson test
data: 14 time base: 1
number of events = 14, time base = 1, p-value = 0.08152
alternative hypothesis: true event rate is not equal to 8.5
95 percent confidence interval:
7.65393 23.48962
sample estimates:
event rate
14
R code is publicly available -- you can check the code; in this case it bears out what I said above.
Glen's answer notes that you can check the code for this function, but I'm not sure if you know how to do this, so I'll augment his answer by showing you how. To check the code, just load the relevant library and type in the function name without any arguments:
library(stats)
poisson.test
function (x, T = 1, r = 1, alternative = c("two.sided", "less",
"greater"), conf.level = 0.95)
{
...some code here...
PVAL <- ...some code...
...more code here...
structure(list(statistic = x, parameter = T, p.value = PVAL,
conf.int = CINT, estimate = ESTIMATE, null.value = r,
alternative = alternative, method = "Exact Poisson test",
data.name = DNAME), class = "htest")
}
}
<bytecode: 0x0000000019efa180>
<environment: namespace:stats>
You will see from the code that the poisson.test function creates a htest object (a list that is classed as a hypothesis test) containing calculations for the test statistic, p-value, and confidence interval. The code is quite long, but a lot of it can be ignored. The parts of interest are the code to calculate the test statistic and p-value, which are about 12-15 lines of code each. You might be able to walk through it and see how each of these objects is calculated, which will tell you the mathematics they are using. This will augment Glen's answer, which confirms the output of the test in a particular case.
