Draw a picture of the integrand.

This plot overlays the area underneath the horizontal line $y=a$ and the area beneath the graph of $y=|x|.$ The union of those areas, weighted by the Normal probability density, is the desired expectation.
One method notes that the expectation of $a$ is $a$ itself, leaving just the probability-weighted areas of the two infinite gray triangles (with vertices at $(\pm a, a)$) to be found.
Thus, writing $a\vee|X|=\max(a,|X|),$ we may integrate over the positive triangle (whose heights are given by $x-a$ for $x\ge a$) and use the fact that $-x\phi(x)=\phi^\prime(x)$ for the standard Normal density $\phi$ to obtain
$$E[a\vee|X|] = a + 2\int_a^\infty (x-a)\phi(x)\mathrm{d}x = a + 2\int_a^\infty(-\phi^\prime(x) - a\phi(x))\mathrm{d}x.$$
The right hand side is integrable by sight because $\phi=\Phi^\prime$ (where $\Phi^\prime=\phi$ is the standard Normal cdf).
Using $\lim_{x\to\infty}\phi(x)=0,$ $\lim_{x\to\infty}\Phi(x)=1$ , and $1-\Phi(a) = \Phi(-a),$ we obtain
$$E[a\vee|X|] = a + 2\phi(a) - 2a\Phi(-a).$$
(This result should remind you of Mills' ratio for the Normal distribution, especially upon viewing the correction term after $a$ as being a multiple of $a\phi(a)/\Phi(a) - 1.)$ Indeed, the foregoing calculations are essentially the same as those employed at Expected value of x in a normal distribution, GIVEN that it is below a certain value.)
This plot of the expectation as a function of $a$ compares it to $a$ itself: as expected, as $a$ grows large, most of the probability is where $a\vee |X|=a$ and so the expectation (solid blue curve) rapidly approaches $a$ (dashed red curve). The integral computed above is the difference between those curves.
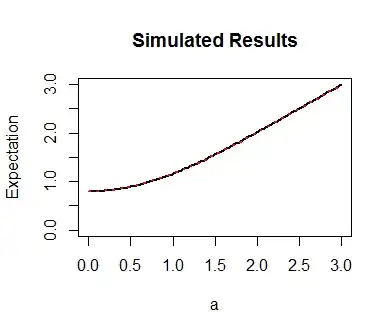
Finally, as a check, here is a quick (sub-second) simulation in R using a million draws from the standard Normal distribution. It plots the theoretical and simulated curves: they are identical.
x <- abs(rnorm(1e6))
sim <- sapply (a <- seq(0, 3, length.out=80), function(a) {
c(mean(pmax(a, x)), a + 2*(dnorm(a) - a * pnorm(-a)))
})
plot(a, sim[2,], type="l", ylim=c(0,3), lwd=2, col="Black",
ylab="Expectation", main="Simulated Results")
lines(a, sim[1,], type="l", ylim=c(0,3), lwd=2, col="Red", lty=3)