2

I am working in R and would like to generate 40 numbers from $\mathrm{N}(0,1)$ and another 40 from $\mathrm{Uniform}(0,2)$ with a negative correlation (for example: $r = -0.45$) between them. The correlation does not have to be exact.

I've done something similar for 2 normally distributed variables by specifying a co-variance matrix - see R code below:

sigma <- matrix(c(.33,-.23,-.23,1), ncol=2, byrow=T)

mu <- c(1,0)

ab <- mvrnorm(n=40, mu, sigma)

One thing I considered was using the above code and then transforming one of the normal variables to a uniform but I am not sure how to go about doing that.

COOLSerdash
  • 25,317
  • 8
  • 73
  • 123
Sandra
  • 21
  • 1

1 Answers1

2

First, sample 40 values from a bivariate normal distribution $(X_1, X_2)^T\sim \mathcal{N}(\mathbf{\mu}, \Sigma)$ with a mean vector of $\mathbf{\mu} = (0, 0)^T$ and covariance matrix $$ \Sigma = \begin{pmatrix} 1 & \rho\sqrt{\frac{\pi}{3}} \\ \rho\sqrt{\frac{\pi}{3}} & 1 \end{pmatrix} $$ where $\rho$ is the desired correlation coefficient between the standard normal and the uniform $\mathrm{U}(0, 2)$ distribution.

Secondly, apply the transformation $Y_1 =\Phi(X_1)$ in order to transform $X_1 $ to a uniform $Y_1\sim \mathrm{U}(0,1)$ distribution. $\Phi$ denotes the CDF of the standard normal distribution.

Multiply $Y_1$ with 2 (i.e. $Z_1=2Y_1$) to get a uniform $Z_1\sim \mathrm{U}(0,2)$ distributed random variable. The variance of $Z_1$ is $\frac{1}{12}(b-a)^2=\frac{1}{12}(2-0)^2=\frac{1}{3}$.

The covariance between $Y_1$ and $X_2$ is $\frac{\rho}{2\sqrt{3}}$. Because $\mathrm{Cov}(aX, Y) = a\mathrm{Cov}(X,Y)$, the covariance between $Z_1$ and $X_2$ is $2\frac{\rho}{2\sqrt{3}}=\frac{\rho}{\sqrt{3}}$. Hence, the correlation between $Z_1$ and $X_2$ is

$$ \mathrm{Corr}(Z_1,X_2)=\frac{\frac{\rho}{\sqrt{3}}}{\sqrt{\frac{1}{3}}\cdot 1} = \rho $$

In R:

library(MASS)

set.seed(142857)

n <- 40

rho <- -0.45 # setting the correlation

sigma <- matrix(c(1, rho*sqrt(pi/3), rho*sqrt(pi/3), 1), 2, 2, byrow = TRUE)

x <- mvrnorm(n, mu = c(0, 0), Sigma = sigma)

z1 <- 2*pnorm(x[, 1])
x2 <- x[, 2]

cor(z1, x2)
[1] -0.4343862

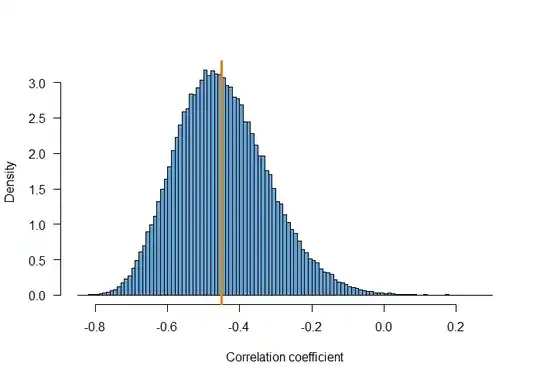
I've simulated $10^5$ repetitions of the above process. The distribution of correlation coefficients between $Z_1$ and $X_2$ is shown here (the vertical orange line denotes the correlation coefficient of $\rho = -0.45$).

Simulation

COOLSerdash
  • 25,317
  • 8
  • 73
  • 123
  • 3
    Is it really that case that `rho` is the correlation of the *resulting* variables or would it merely be the correlation parameter for the bivariate Normal distribution that underlies the copula? I suspect it would be the latter, but this question asks for the former. – whuber Jul 01 '19 at 21:35
  • @whuber Good question. I think you're right. My simulations show that the mean of the resulting correlations is not $-0.45$ which is troublesome. A the moment, I'm unable to fully grasp and explain why. I will leave the answer up for the moment but will delete it when a better one is posted. – COOLSerdash Jul 02 '19 at 09:43
  • 2
    The reason for the discrepancy is that the transformation of the marginal uniform distribution to a marginal Normal distribution is nonlinear and therefore is likely to change the correlation. However, it's not "strongly" nonlinear and therefore changes the correlation only a little, in a way that varies with $\rho.$ One could study this variation (in this particular case) and thereby produce the function that translates the value of $\rho$ into the correlation. The problem would then be solved by inverting that function. – whuber Jul 02 '19 at 13:37
  • @whuber I believe that the correlation after the transformation is $\sqrt{3/\pi}\rho$. Therefore, multiplying $\rho$ with $\sqrt{\pi/3}$ should give the desired calculations after transformation. – COOLSerdash Jul 02 '19 at 16:26