Nonlinear sin model with brms

Question

I try to fit sin function with brms using next code:

library(tidyverse)
library(brms)

N <- 100
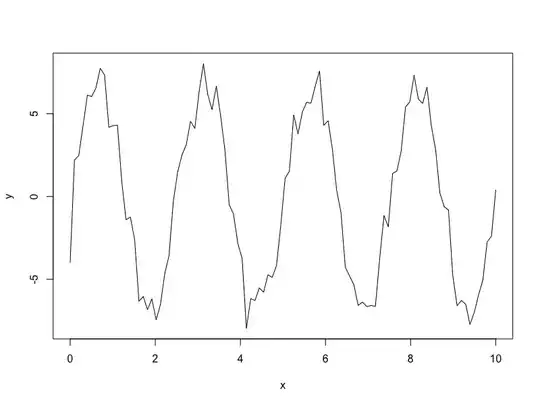
x <- seq(0, 10, length.out = N)
e <- rnorm(N)
y <- 7 * sin(2.5 * x) + e
inp_data <- tibble(x, y)
plot(inp_data, type = 'l')

priors <- prior(normal(7, 100), nlpar = "a") +
  prior(normal(2.5, 100), nlpar = "b")

sin_fit <- brm(bf(y ~ a * sin(b * x), a + b ~ 1, nl = TRUE),
               data = inp_data, prior = priors, refresh = 0)

The result is:

summary(sin_fit)

The model has not converged (some Rhats are > 1.1). Do not analyse the results!
We recommend running more iterations and/or setting stronger priors. 
Family: gaussian
Links: mu = identity; sigma = identity
Formula: y ~ a * sin(b * x) 
         a ~ 1
         b ~ 1
Data: inp_data (Number of observations: 100)
Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
         total post-warmup samples = 4000

Population-Level Effects:
Estimate Est.Error l-95% CI u-95% CI Eff.Sample   Rhat
a_Intercept     -0.00      6.83    -7.06     7.07          2  51.50 
b_Intercept     -0.00      2.51    -2.51     2.51          2 762.60

Family Specific Parameters: 
Estimate Est.Error l-95% CI u-95% CI Eff.Sample Rhat
sigma     1.00      0.07     0.87     1.16       2902 1.00

Samples were drawn using sampling(NUTS). For each parameter, Eff.Sample is
a crude measure of effective sample size, and Rhat is the potential scale 
reduction factor on split chains (at convergence, Rhat = 1).

plot(sin_fit)

How to get the right values (a = 7 and b = 2.5)? What kind of prior should I use?

Did you also ask this on the Stan forums? https://discourse.mc-stan.org/ They might be better able to help with these Stan-ecosystem-specific questions. — Maurits M, Jun 24 '19 at 12:22
Because $a\sin(bx)=(-a)\sin((-b)x),$ your model is not identifiable. This is very clear in the top two graphical rows of your output. — whuber, Jun 24 '19 at 12:50
Oh that is an excellent point by whuber - you can probably fix this with tighter priors (for instance, priors that have most of their mass above zero). Hope this helps! — Maurits M, Jun 24 '19 at 14:02
Thanks to everybody! I've used positive constrained priors but not Cauchy distribution. — user2579566, Jun 26 '19 at 09:44

Demetri Pananos · Accepted Answer · 2019-06-26T00:46:43.063

A whuber said, your model is not identifiable because of the oddity of sine.

If, however, you impose weakly informative priors supported on the positive reals, then some nice stuff results.

Note, I've changed your priors to something a little more sane.

library(tidyverse)
library(brms)

N <- 100
x <- seq(0, 10, length.out = N)
e <- rnorm(N)
y <- 7 * sin(2.5 * x) + e
inp_data <- tibble(x, y)

priors <- prior(cauchy(0, 1), nlpar = "a", lb = 0) +
  prior(cauchy(0, 1), nlpar = "b", lb = 0)  +
  prior(cauchy(0,1), class = 'sigma' )

sin_fit <- brm(bf(y ~ a * sin(b * x), a + b ~ 1, nl = TRUE),
               data = inp_data, prior = priors, refresh = 0)

plot(sin_fit)

And here is the result of the fit (true in black, estimate in blue)

Thank you very much Demetri! – user2579566 Jun 26 '19 at 13:10 — user2579566, Jun 26 '19 at 13:10

Nonlinear sin model with brms

1 Answers1