0

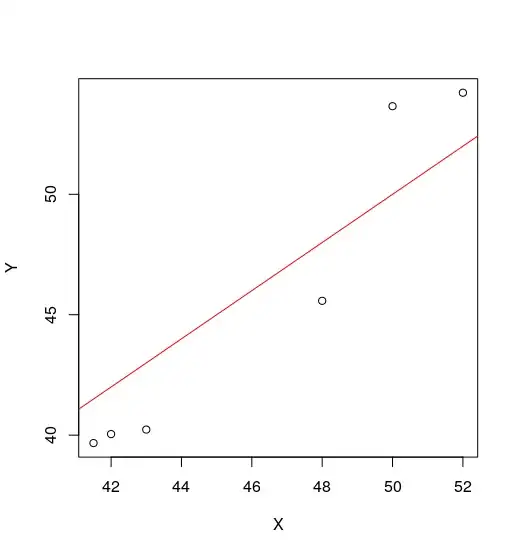
I have this bit of data :

Y <- c(40.2304958024139,53.6587545658805,39.6709850206028,
       45.5769321619423, 54.2182653476916, 40.0439922084769)

X <- c(43, 50, 41.5, 48, 52, 42)

and want to get the average transformation from $X$ to $Y$. My obvious choice was a simple lm in R to get the coefficients and be on my merry way. However, this is what pops out of the lm function:

> summary(lm(Y~X))

Call:
lm(formula = Y ~ X)

Residuals:
       1        2        3        4        5        6 
-0.79894  2.32880  0.84880 -2.81002 -0.05469  0.48606 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)   
(Intercept)  -22.245      8.881  -2.505  0.06643 . 
X              1.472      0.192   7.666  0.00156 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1.931 on 4 degrees of freedom
Multiple R-squared:  0.9363,    Adjusted R-squared:  0.9203 
F-statistic: 58.76 on 1 and 4 DF,  p-value: 0.001557

Now, I'm aware these are probably the best parameters for this data, but since the whole aim of getting that transformation in the first place is to apply it to a set of larger $X$s, subtracting $22$ and then multiplying by $1.5$ will certainly not scale.

Is there a way I can constrain the parameters such that I get a reasonable intercept and slope ? This data is reasonably close to $Y=X$, so I was expecting a slope nearer to $1$ and intercept closer to $0$.

RoB
  • 143
  • 7
  • 1
    You really need to tell us more about your data. At this moment you seem to be telling us that linear regression doesn't work for your data because linear model is not suitable for your data. It is unclear what is "ridiculous" about this intercept and what kind of intercept wouldn't be "ridiculous". – Tim Jun 14 '19 at 15:03
  • Ah, sorry. I mean that since this data is already very close to $Y=X$, having such parameters clearly seems wrong ! I'll edit my question. – RoB Jun 14 '19 at 15:06
  • Would a Bayesian approach, w/ a strong prior on $0$ & $1$, be acceptable? – gung - Reinstate Monica Jun 14 '19 at 15:14
  • Well, probably but it seems like way overkill for this... – RoB Jun 14 '19 at 15:15

1 Answers1

0

Have you tried plotting this data?

enter image description here

If there was $Y=X$ relation, we would expect to see points lying along the line. I plotted your data with the $\beta_0=0$ and $\beta_1=1$ regression parameters, and as you can see, neither of the points lies on the line. You could try drawing several different lines, or curves, that would fit those points better. Even if there is strong linear relation between the points, then you have not enough data to predict it.

If you have some prior knowledge that suggests that the parameters should be close to $\beta_0=0$ and $\beta_1=1$, then this sounds like a clear case for using Bayesian linear regression.

Tim
  • 108,699
  • 20
  • 212
  • 390
  • Yes, I've actually been staring at that exact plot for the past half hour ! Thank you for the tip, I'll look into the Bayesian linear regression. – RoB Jun 14 '19 at 15:27