How is it possible to control for observer bias in measurements with a random effect?

Question

I have a dataset with repeated (but not always) measures of animals. I need to control for observer bias in measuring the morphology of my animal. I'm wondering what is the way to first estimate repeatability, and then correct the measurements of the animals based on the most repeatable observer.

Below, I tried to write a script that would do that, but estimating repeatability is not giving me what I expect.

In the script below, I simulated 2 people (John and Emily) measuring 20 times the same organism (10 each). I created the data so that they should be very repeatable.

#Load the package
library(rptR)

# Make fake data 
animal.id = rep(LETTERS,each=10)
obs = c(rep(c("John","Emily"),130),
        rep(c("John","Emily"),130))
meas = abs(rnorm(length(obs), mean = 14, sd = 1))

# put data in data.frame 
data = data.frame(animal.id,obs, meas)
# Order the data to see the differences in measurement of the same animal 
data = data[order(data[,c("animal.id")],data[,c("obs")]),]

# Add different values to each observer (test for differences in measuring the same animal)
data[data$obs=="John","meas"] <- data[data$obs=="John","meas"] + rnorm(26, mean = 1,sd = 0)
data[data$obs=="Emily","meas"] <-data[data$obs=="Emily","meas"] + rnorm(26, mean = 1,sd = 0)

# Define parameters 
nboot = 100
npermut = 100

# Find repeatability 
x1=rpt(meas ~ 1 + (1|animal.id),
       grname = c("animal.id"),
       data = data,
       datatype ="Gaussian", 
       nboot = nboot, 
       npermut=npermut)
plot(x1)
x1

This is the result from the script above:

Repeatability estimation using the lmm method 

Repeatability for animal.id
R  = 0
SE = 0
CI = [0, 0]
P  = 0.5 [LRT]
     0.38 [Permutation]

This means that they are not repeatable. So, is there a way to find the repeatability per observer and then correct the actual measurements based on the most repeatable observer?

I guess that if someone adds always 1mm to the measured trait this could be corrected in the raw data.

Maybe I'm interpreting this wrong, and when people say that they "correct" the measurement based on repeatability, they just put a random effect of observer and it accounts for the variability that observer put in the response.

EDIT

I made a new script and found that the function ranef might be useful

# Make fake data 
animal.id = c(rep(LETTERS,each=10),"C")
obs = c(rep(c("John","doh","Emily"),43),
        rep(c("John","doh","Emily"),44))

# put data in data.frame 
data = data.frame(animal.id,obs#, meas
                  )
data$meas = NA
ani.id = unique(animal.id)
for (i in 1:length(ani.id)) {
  # Extract a phenotype from the population phenotype distribution
  pop.dist = rnorm(n = 1,
                   mean = 14,
                   sd = 1)
  rowss = which(data$animal.id == ani.id[i])
  # Make a certain individual a certain value 
  data[rowss,"meas"] <- rnorm(n = length(rowss), 
                              mean = pop.dist,
                              sd = 0)
}

# Order the data to see the differences in measurement of the same animal 
data = data[order(data[,c("animal.id")], data[,c("obs")]),]



# Add different values to each observer (test for differences in measuring the same animal)
data[data$obs=="John","meas"] <- data[data$obs=="John","meas"] + rnorm(length(data[data$obs=="John","meas"]), 
                                                                       mean = 2,sd = 0.5)
data[data$obs=="doh","meas"] <- data[data$obs=="doh","meas"] + rnorm(length(data[data$obs=="doh","meas"]), 
                                                                     mean = 5,sd = 0.8)
data[data$obs=="Emily","meas"] <-data[data$obs=="Emily","meas"] + rnorm(length(data[data$obs=="Emily","meas"]), 
                                                                        mean = 0,sd = 0.7)


library(lme4)
x2 = lmer(meas ~ (1|obs)+ (1|animal.id), data = data )
x3 = lmer(meas ~ -1 + obs+ (1|animal.id), data = data )
x4 = lmer(meas ~ obs + (1|animal.id), data = data )
summary(x2)
x2
icc(x2)
round(fixef(x2))
round(fixef(x3))
round(fixef(x4))
fixef(x4)
ranef(x2)$obs
rr1=ranef(x2, condVar = TRUE)
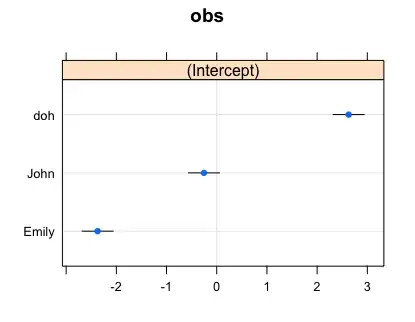
dotplot(rr1)

I think this is pretty convincing now. From model 4 lmer(meas ~ obs + (1|animal.id), data = data), the fixed effect looks like this:

round(fixef(x4))
(Intercept)    obsEmily     obsJohn 
         19          -5          -3

Here is the simulation:

John  (mean = 2, sd = 0.5)
doh   (mean = 5, sd = 0.8)
Emily (mean = 0, sd = 0.7)

This means that Intercept is the population mean (pop.dist = rnorm(n = 1, mean = 14, sd = 1)) plus the increase in measure that "doh" is adding (5). John compared to doh adds -3 (2 from the population mean) and Emily adds nothing (-5) compared to doh (5).

The script below calculates the repeatability of each observer.

# Define parameters 
nboot = 100
npermut = 100
my.list = NULL

# Find repeatability 
measurer = levels(data$obs)
for(i in 1:length(measurer)){
  # How many measures were done by this guy
  tmp  = data[data$obs==measurer[i],]
  x1=rpt(meas ~ 1 + (1|animal.id),
         grname = c("animal.id"),
         data = tmp,
         datatype ="Gaussian", 
         nboot = nboot, 
         npermut=npermut)
  plot(x1)
my.list = c(my.list,list(x1))
  print(x1)
}
my.list

Here is the answer to the repeatability!

[[1]]
Repeatability estimation using the lmm method 
Repeatability for animal.id
R  = 0.588
SE = 0.109
CI = [0.349, 0.743]
P  = 1 [LRT]
     0.01 [Permutation]

[[2]]
Repeatability estimation using the lmm method 
Repeatability for animal.id
R  = 0.631
SE = 0.082
CI = [0.449, 0.767]
P  = 1 [LRT]
     0.01 [Permutation]

[[3]]
Repeatability estimation using the lmm method 
Repeatability for animal.id
R  = 0.819
SE = 0.051
CI = [0.668, 0.883]
P  = 1 [LRT]
     0.01 [Permutation]

EDIT2

I noticed that based on the information that we have on an animal, it might be better to use the most relevant biological value for the "correction" of the phenotypic measurements.

mean.not.corrected=mean(data$meas)

data$obs = factor(data$obs,levels(data$obs)[c(2,1,3)])
meas.eff = fixef(x4)
data[data$obs=="doh","meas"] = data[data$obs=="doh","meas"]-meas.eff[2]
data[data$obs=="John","meas"] = data[data$obs=="John","meas"]-meas.eff[3]
mean(data$meas)
x5 = lmer(meas ~ (1|obs)+ (1|animal.id), data = data )
x6 = lmer(meas ~ -1 + obs+ (1|animal.id), data = data )
x7 = lmer(meas ~ obs + (1|animal.id), data = data )

round(fixef(x5))
round(fixef(x6))

mean.corrected = mean(data$meas)

As you can see the corrected mean (13.7) is closer to the population mean (14) compared to the uncorrected mean is 16.1.

mean.corrected
[1] 13.709
mean.not.corrected
[1] 16.11122

Here you can see that there is no difference between the observers:

round(fixef(x7))
(Intercept)      obsdoh     obsJohn 
         14           0           0

You can now see that there is no random effect.

ranef(x5)
$obs
      (Intercept)
Emily           0
doh             0
John            0

EDIT 3

# In the parametric world
hist(data$meas)
av.out1 = aov(meas ~ obs + animal.id, data=data)
av.out2 = aov(meas ~ obs, data=data)

summary(av.out1)
TukeyHSD(av.out1,"obs")
TukeyHSD(av.out2,"obs")

# In the non parametric framework, there is no difference  (Mann-Whitney-Wilcoxon Test)
nonpar.data1 = data[data$obs %in% c("John","Emily") ,]
nonpar.data2 = data[data$obs %in% c("John","doh") ,]
nonpar.data3 = data[data$obs %in% c("doh","Emily") ,]
wilcox.test(meas ~ obs, data=nonpar.data1) 
wilcox.test(meas ~ obs, data=nonpar.data2) 
wilcox.test(meas ~ obs, data=nonpar.data3) 

# There is no difference in the non-parametric Kruskal-Wallis Test
kruskal.test(meas ~ obs, data = data)

Does that make sense?

It is trivial in lmer to add additional random effect to your model. Have you tried this? You could then calculate an ICC for animal and observer to get a sense of how much variation in the response is contained in each of these groups. Can you do that and report back? — Erik Ruzek, Jun 07 '19 at 21:11
I've done this: ```library(lme4); x2 = lmer(meas ~ (1|obs)+ (1|animal.id), data = data ); summary(x2); icc(x2) ``` This is the answer: Linear mixed model Family : gaussian (identity) Formula: meas ~ (1 | obs) + (1 | animal.id) ICC (animal.id): 0.0000 ICC (obs): 0.9073 I made it so there is a difference of "4" (meaning that "John" will always measure 4 units more than Emily) in the measurement from the 2 observers — M. Beausoleil, Jun 07 '19 at 21:18
Perhaps, just putting the "obs" as a random effect is fine as it would take into account the variance of obs into the model: ```ranef(x2)$obs``` gives this table: (Intercept) Emily -2.065328 John 2.065328 — M. Beausoleil, Jun 07 '19 at 21:30
I think that is the case. As I increase the measurement difference between John and Emily, I get the exact difference if I calculate ```sum(abs(ranef(x2)$obs))```. — M. Beausoleil, Jun 07 '19 at 21:32
Did you specify 0 variance due to animals in your simulated data? That would be very weird in reality. — Erik Ruzek, Jun 07 '19 at 21:36
Yes I did that (0 variance), but just to see what would happen (I wanted to isolate the effect of the observer). With ```sum(ranef(x2)$obs)``` this value (I think) should equal ```0```. That's what I'm getting if I add a little variation in the measurement for everyone and then see if there is a systematic bias for each observer. But then, do I need to do something on the original data? Or this is accounted by itself into the model? — M. Beausoleil, Jun 07 '19 at 21:41
The approach of a random intercept for observer will account for that issue. You do not need to add any additional noise to their scores. Note that if you have a small number of observers (e.g., <10), you may want to include dummy variables for the observer vs. an observer random effect. Go with what is customary in your field on this issue. — Erik Ruzek, Jun 07 '19 at 21:52
"Note that if you have a small number of observers (e.g., <10), you may want to include dummy variables for the observer vs. an observer random effect" What do you mean by "dummy variables" ? — M. Beausoleil, Jun 10 '19 at 15:12
Sorry for not being clearer. Create 0/1 indicators (dummy variables) for each of the observers. Add those 0/1 indicators as predictors to your model. Unless you suppress a constant, you will have to leave out one of the indicator variables, so you would add nine 0/1 indicator variables for your observers. — Erik Ruzek, Jun 10 '19 at 21:50

How is it possible to control for observer bias in measurements with a random effect?

0 Answers0