How to perform t-test with huge samples?

Question

I have two populations, One with N=38,704 (number of observations) and other with N=1,313,662. These data sets have ~25 variables, all continuous. I took mean of each in each data set and computed the test statistic using the formula

t=mean difference/std error

The problem is of the degree of freedom. By formula of df=N1+N2-2 we'll have more freedom than the table can handle. Any suggestions on this? How to check the t statistic here. I know that the t-test is used for handling samples but what if we apply this on large samples.

Answer 1

chl already mentioned the trap of multiple comparisons when conducting simultaneously 25 tests with the same data set. An easy way to handle that is to adjust the p value threshold by dividing them by the number of tests (in this case 25). The more precise formula is: Adjusted p value = 1 - (1 - p value)^(1/n). However, the two different formulas derive almost the same adjusted p value.

There is another major issue with your hypothesis testing exercise. You will most certainly run into a Type I error (false positive) whereby you will uncover some really trivial differences that are extremely significant at the 99.9999% level. This is because when you deal with a sample of such a large size (n = 1,313,662), you will get a standard error that is very close to 0. That's because the square root of 1,313,662 = 1,146. So, you will divide the standard deviation by 1,146. In short, you will capture minute differences that may be completely immaterial.

I would suggest you move away from this hypothesis testing framework and instead conduct an Effect Size type analysis. Within this framework the measure of statistical distance is the standard deviation. Unlike the standard error, the standard deviation is not artificially shrunk by the size of the sample. And, this approach will give you a better sense of the material differences between your data sets. Effect Size is also much more focused on confidence interval around the mean average difference which is much more informative than the hypothesis testing focus on statistical significance that often is not significant at all. Hope that helps.

Answer 2

Student's t-distribution becomes closer and closer the the standard normal distribution as the degrees of freedom get larger. With 1313662 + 38704 – 2 = 1352364 degrees of freedom, the t-distribution will be indistinguishable from the standard normal distribution, as can be seen in the picture below (unless perhaps you're in the very extreme tails and you're interested in distinguishing absolutely tiny p-values from even tinier ones). So you can use the table for the standard normal distribution instead of the table for the t-distribution.

Answer 3

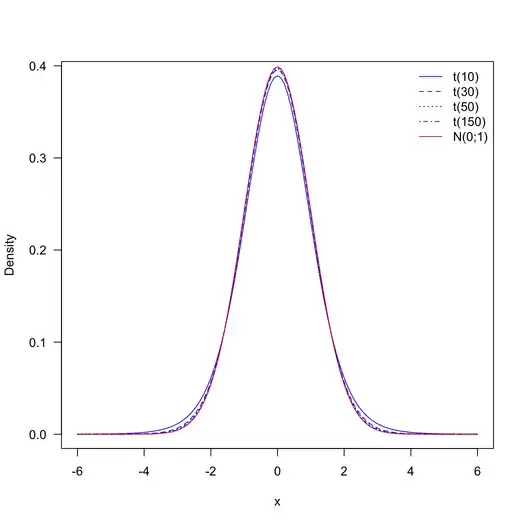
The $t$ distribution tend to the $z$ (gaussian) distribution when $n$ is large (in fact, when $n>30$, they are almost identical, see the picture provided by @onestop). In your case, I would say that $n$ is VERY large, so that you can just use a $z$-test. As a consequence of the sample size, any VERY small differences will be declared significant. So, it is worth asking yourself if these tests (with the full data set) are really interesting.

Just to be sure, as your data set includes 25 variables, you are making 25 tests? If this is the case, you probably need to correct for multiple comparisons so as not to inflate the type I error rate (see related thread on this site).

BTW, the R software would gives you the p-values you are looking for, no need to rely on Tables:

> x1 <- rnorm(n=38704)
> x2 <- rnorm(n=1313662, mean=.1)
> t.test(x1, x2, var.equal=TRUE)

    Two Sample t-test

data:  x1 and x2 
t = -17.9156, df = 1352364, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0 
95 percent confidence interval:
 -0.1024183 -0.0822190 
sample estimates:
  mean of x   mean of y 
0.007137404 0.099456039 

Answer 4

You can use the following python function which I wrote, that can calculate the size effect. The test is straightforward here

import numpy as np 
from scipy.stats import t

def Independent_tTest(x1, x2, std1, std2, n1, n2): 
    '''Independent t-test between two sample groups

    Note: 
        The test assumptions:
            H0: The two samples are not significantly different (from same population)
            H1: The two samples are siginficantly different (from two populations)
            - Accept the H1 if t-value > t-critical or p-value value < p-value critical
    Args: 
        x1(float): mean of the first sample group.
        x2(float): mean of the second sample group.
        std1(float): standard deviation of first sample group.
        std2(float): standard devation of second sample group.

    Return: 
        degree_of_freedome, t-statistics, p-value

    '''
    degree_of_freedom = n1 + n2  -2
    corrected_degree_of_freedom = (((std1**2/n1) + (std2**2/n2))**2)/(((std1**4)/((n1**2)*(n1-1)))+((std2**4)/((n2**2)*(n2-1))))

    poolvar = ((n1-1)*(std1**2)+ (n2-1)*(std2**2))/corrected_degree_of_freedom
    t_value = (x1 -x2)/np.sqrt(poolvar*((1/n1)+ (1/n2)))
    sig = 2 * (1-(t.cdf(abs(t_value), corrected_degree_of_freedom)))
    effect_size = np.sqrt((t_value**2)/(t_value**2+corrected_degree_of_freedom))
    return f"corrected degree of freedom {corrected_degree_of_freedom:0.4f} give a t-value = {t_value:0.4f}, with significant = {sig:0.4f} with effectsize ={effect_size:0.4f}"