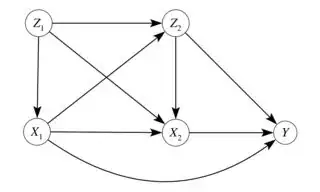
Conditional expectation $E[Y|X]$ and interventional expectation $E[Y|do(X)]$ are related but conceptually very different things.
I know that if $X$ is a randomly assigned by an experiment, we have that $E[Y|X]=E[Y|do(X)]$ In some other case we can achieve the equivalence by conditioning on proper set of variables $Z$: $E[Y|X,Z]=E[Y|do(X)]$
My question: is possible to consider both $X$ and $Z$ as vector of variables? Usually in an experiment we are focused in just one causal variable ($X$ as scalar), however logically seems me that the generalization is permitted.