GARCH(1,1) volatility forecast looks biased, it is consistently higher than Parkinson's HL vol

Question

I am trying to create one-step ahead forecasts for the S&P500 using a GARCH(1,1) model. I am using the rugarch package in R.

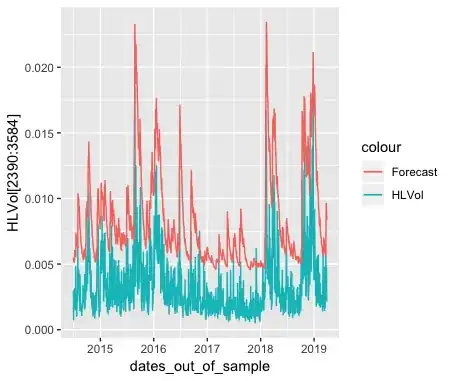
As you can see, the forecasted points are consistently higher than the volatility suggested by Parkinson's HL volatility formula. I have also checked Realized Volatility measures using 5-min intraday data, and I found that it is very close to the Parkinson HL.

I found that if I adjust the Parkinson's HL vol by 0.0025, it fits very close to the volatility suggested by the GARCH(1,1) model.

What could be the issue that makes the GARCH model volatility forecasts higher?

library(quantmod)
library(xts)
library(forecast)
library(rugarch)
library(fGarch)
library(tseries)
library(ggplot2)
###########################################################
###########################################################
df <- getSymbols("^GSPC",auto.assign = FALSE, from = "2004-12-31", to= "2019-03-31")
price = coredata(df$GSPC.Adjusted)
df$logret <- diff(log(df$GSPC.Adjusted))
logreturns = df$logret[-1,]
df2<-df[2:3585]
T <- nrow(logreturns)
T_train <- round(2/3*T)
T_test <- T - T_train
dates_out_of_sample <- tail(index(logreturns), T_test)
dates_all <- index(logreturns)
dates_in_sample <- dates_all[1:T_train]

model1=ugarchspec(
  variance.model = list(model = "sGARCH", garchOrder = c(1, 1)),
  mean.model = list(armaOrder = c(0, 0), include.mean = TRUE),
  distribution.model = "norm")

garch1.fit <- ugarchfit(spec=model1,data=logreturns, out.sample = T_test)

garch1.forecast <- ugarchforecast(garch1.fit, n.ahead = 1, n.roll = T_test - 1 )

garch1.volforecast <- t(garch1.forecast@forecast[["sigmaFor"]])

HLVol <- (log(df$GSPC.High[2:3585]) - log(df$GSPC.Low[2:3585]))/(4*log(2))

I think most of the library calls can be deleted without affecting the code. Also, what element of `garch1.forecast` do we see in the plot? Moreover, why do you think it is GARCH rather than Parkinson that is biased? (I am not necessarily challending this, just asking for clarification.) — Richard Hardy, May 05 '19 at 08:36
May it be that you are comparing $\hat\sigma_t$ from GARCH with $\hat\sigma_t^2$ from Parkinson? The reason I mentioned library calls is precisely because they are irrelevant, so it would be easier to read the code without them. — Richard Hardy, May 05 '19 at 09:19

score 3 · Accepted Answer · answered May 05 '19 at 10:36

3

This "bias" is simply a result of comparing open-to-close variance (realized measures of volatility) with close-to-close variance (GARCH model).

You could try to:

Use open-to-close returns in the GARCH model
Add overnight return to the realized measure
Correcting the realized measure using a formula like

$$ \hat{\sigma}^2_t = k\cdot RM_t $$ where $RM_t$ is the realized measure and

$$ k = \frac{\sum_{t=1}^T r_t^2}{\sum_{t=1}^T RM_t} $$

answered May 05 '19 at 10:36

Johan Stax Jakobsen

1,035
1
7
15

Interesting point, never thought of that (never worked with measures of realized volatility, so no wonder). – Richard Hardy May 05 '19 at 10:52
Yes - I never had either before I worked with the Realized GARCH models. – Johan Stax Jakobsen May 05 '19 at 11:05
Thank you very much for your answer, very informative. I will look into which of these options will work best for this project. – Tommy May 05 '19 at 11:20

GARCH(1,1) volatility forecast looks biased, it is consistently higher than Parkinson's HL vol

1 Answers1

Linked