Finding the MLE of Poisson in R

Question

I'm trying to determine the MLE of $\lambda$ in a Poisson distribution using R. I'm aware that the MLE is $\hat{\lambda}=\bar{x}$ but I want to demonstrate this using Rmarkdown. My experience with R code is limited and I wish to learn how to do this, but all reference material I have found involves actually generating frequencies and such which I do not wish to do. Are there any references for learning how determine the MLE in R without making use of a sample of data?

Answer 1

Well, if there's no data involved then it seems like a pen and paper would do the trick, since the MLE will be the same no matter what. I don't think R will prove very useful to you, but it would be easy to show your calculations in Rmarkdown. Here's what it could look like:

"The PMF for the Poisson distribution is as follows: $$\frac{\lambda^xe^{-\lambda}}{x!}$$ We want to find the estimate for $\lambda$ that is most likely given the data. The joint PMF for the data (assuming independent observations) is: $$\Pi_{i=1}^{n}\frac{\lambda^{x_i}e^{-\lambda}}{x_i!}$$ when there are $n$ observations. This is the likelihood. It will be easier to find the value of $\lambda$ that maximizes this quantity if we take the log: $$\log (\Pi_{i=1}^{n}\frac{\lambda^{x_i}e^{-\lambda}}{x_i!}) = \sum_{i=1}^{n}\log(\frac{\lambda^{x_i}e^{-\lambda}}{x_i!}) = \sum_{i=1}^n x_i\log(\lambda) - \sum_{i=1}^n \lambda - \sum_{i=1}^n \log (x_i!)$$ $$=\log(\lambda)\sum_{i=1}^nx_i - n\lambda - \sum_{i=1}^n \log (x_i!)$$ To find the value of $\lambda$ that maximizes this equation, we take the derivative, set the derivative equal to zero, and solve for $\lambda$: $$0 = \frac{1}{\lambda}\sum_{i=1}^nx_i - n$$ $$n\lambda = \sum_{i=1}^n x_i$$ $$\lambda = \frac{\sum_{i=1}^n x_i}{n} = \bar{x}$$"

The syntax used to produce this is:

The PMF for the Poisson distribution is as follows: $$\frac{\lambda^xe^{-\lambda}}{x!}$$ We want to find the estimate for $\lambda$ that is most likely given the data. The joint PMF for the data (assuming independent observations) is: $$\Pi_{i=1}^{n}\frac{\lambda^{x_i}e^{-\lambda}}{x_i!}$$ when there are $n$ observations. This is the likelihood. It will be easier to find the value of $\lambda$ that maximizes this quantity if we take the log: $$\log (\Pi_{i=1}^{n}\frac{\lambda^{x_i}e^{-\lambda}}{x_i!}) = \sum_{i=1}^{n}\log(\frac{\lambda^{x_i}e^{-\lambda}}{x_i!}) = \sum_{i=1}^n x_i\log(\lambda) - \sum_{i=1}^n \lambda - \sum_{i=1}^n \log (x_i!)$$ $$=\log(\lambda)\sum_{i=1}^nx_i - n\lambda - \sum_{i=1}^n \log (x_i!)$$ To find the value of $\lambda$ that maximizes this equation, we take the derivative, set the derivative equal to zero, and solve for $\lambda$: $$0 = \frac{1}{\lambda}\sum_{i=1}^nx_i - n$$ $$n\lambda = \sum_{i=1}^n x_i$$ $$\lambda = \frac{\sum_{i=1}^n x_i}{n} = \bar{x}$$"

Answer 2

If $n = 10$ and $T = \sum_{i=1}^n X_i = 85,$ then the likelihood is proportional to $\lambda^T e^{-n\lambda}.$ The likelihood function is maximized at MLE $\hat\lambda =T/n= 8.5,$ as illustrated in R:

n = 10;  t = 85;  lam = seq(1, 15, by=.01)
like = dpois(t, n*lam)
plot(lam, like, type="l", lwd=2)
  abline(v = 8.5, col="red")

lam[like==max(like)]
[1] 8.5                # MLE

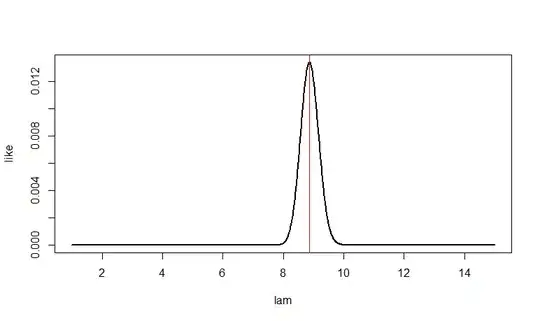
By contrast, if $n=100, T = 887,$ then $\hat \lambda = 8.87.$ There is more data, so the likelihood function near $\hat \lambda$ is more tightly curved, and the estimate is less variable.

n = 100;  t = 887;  lam = seq(1, 15, by=.01)
like = dpois(t, n*lam)
plot(lam, like, type="l", lwd=2)
  abline(v = 8.87, col="red")

lam[like==max(like)]
[1] 8.87