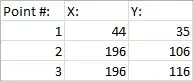Ripley K function value in a specific radius and dataset using R's Kest function

Question

I'm having general trouble with calculating Ripley's K function values.

The following is a simple spatial point pattern, where both X and Y range from 0 to 200:

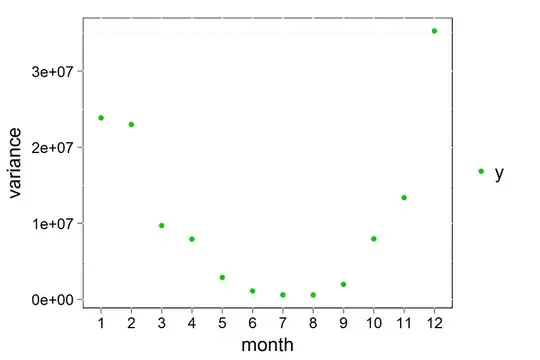
Here's its corresponding Ripley K chart in R:

The problem is, I'm completely failing to understand how does R get K(10) ~ 21000.

Here's my step by step solution:

The Ripley K function, according to "Spatial point pattern analysis of available and exploited resources", Lancaster, Downes, 2004, is defined as: $$K(r) = {n^{-2}A \sum_{i}^n \sum_{j\ne i}^n w_{ij}I_r(u_{ij})}$$

Where:

• n is the amount of points (3),
• A is the domain area (200x200 = 40000),
• w is the weighting factor, which I understand as the ratio of actual area of the sphere centered in the point i, which is contained within the bounds of the domain, to the area of a sphere centered in the point i.,
• u is the distance between points i and j,
• I is the indicator function, which should be set to 1, if u is smaller or equal to radius, and 0 otherwise.

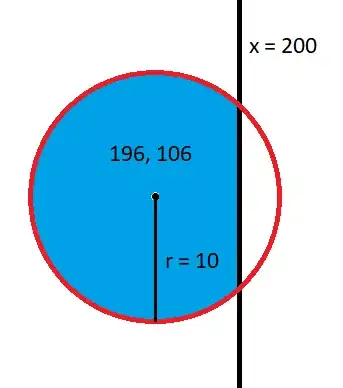
First off, let's calculate the weights: Weight of point #1 obviously equals 1. However, #2 and #3 are near the domain edge, and since they have the same x coordinate, and aren't near the upper boundaries, they're going to be equal.

The weight will be the blue, boundary area divided by the area of the red sphere. Boundary area is equal to the area of the red sphere minus the area of the white circular segment.

The circular segment's area equals exactly 79.27, so:

$$w_{2,1}=w_{2,3}=w_{3,1}=w_{3,2}= {\pi10^2-79.27\over \pi10^2}={234.73\over 314}\approx0.75$$

Only the points #2 and #3 are within each other's radius, so the indicator function will be set to 1 only twice: between #2 and #3 and vice versa.

So the final result should be:

$$K(r)=3^{-2}\cdot40000 \cdot(1\cdot0+1\cdot0+0.75\cdot0+0.75\cdot1+0.75\cdot0+0.75\cdot1)=\\=4444.(4)\cdot1.5=6666.(6)$$

Which is vastly smaller than R's ~21000.

Also, the Kest function has a different definition of K function:

Kest(r) = (a/(n * (n-1))) * sum[i,j] I(d[i,j] <= r) e[i,j])

In that case:

$$Kest(r)=(40000/(3\cdot(3-1)))\cdot1.5=10000$$

Also wrong.

What am I doing wrong here? Is this some simple math mistake I've made somewhere, or is there something about R's Kest function that I'm missing?

Answer 1

Once again: Thank you for a detailed and well written question. The main points are:

• The weights are given in terms of circumference and not area.
• The weights are greater than or equal to 1 (inverses of what you describe – with area replaced by circumference).
• You can find the weights in spatstat using edge.Ripley().

The following example has two points separated by r = 1 with 1/4 of the circumference outside the 10x10 window (i.e. area 100). Thus the value should jump from 0 to 100/(2 ⋅ 1) ⋅ ((3/4)^− 1 + (3/4)^− 1) = 100 ⋅ 4/3 = 133.333.

library(spatstat)
x <- c(4.5,5.5)
y <- c(10,10)-sqrt(2)/2
W <- square(10)
X <- ppp(x, y, W)
plot(X %mark% 1, markscale = 2, main = "", legend = FALSE)

Kfun <- Kest(X, correction = "iso")
plot(Kfun)

Kval <- as.data.frame(Kest(X, correction = "iso"))
Kval[Kval$r>.99 & Kval$r<1.01,]
#>             r     theo      iso
#> 204 0.9912109 3.086612   0.0000
#> 205 0.9960938 3.117097   0.0000
#> 206 1.0009766 3.147732 133.3333
#> 207 1.0058594 3.178516 133.3333
edge.Ripley(X, c(1,1))
#>          [,1]
#> [1,] 1.333333
#> [2,] 1.333333

^{Created on 2019-03-21 by the reprex package (v0.2.1)}