1

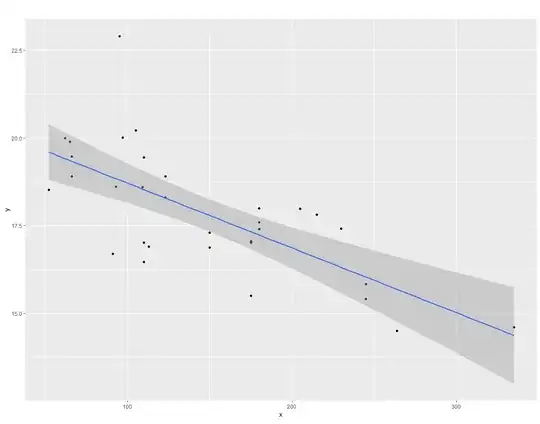
If I have two variables x and y that have a linear relationship e.g. using data from the mtcars package and R code

df <- mtcars[c(4,7)]
names(df) <- c("x", "y")

model <- lm(y~x, data = df)

p <- ggplot(data = df, aes(x,y)) +
  geom_point() +
  stat_smooth(method = "lm")

enter image description here

if I've test that my model doesn't violate any of the assumptions of lm, for each value of x there exists some distribution of y with a mean on the best fit line for the linear regression.

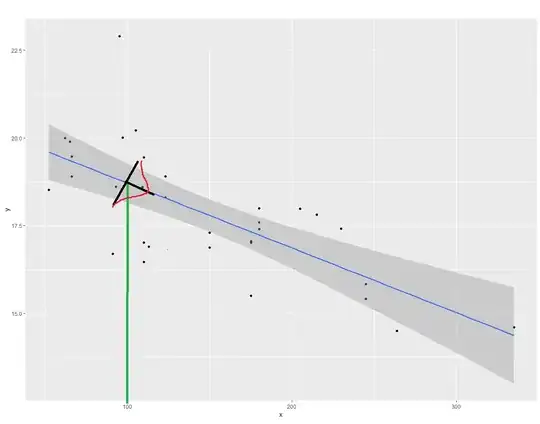
e.g. if I have a some thing with an x = 100 then my expected value of y will be ~ 18.75, but there will be some pdf around this

enter image description here

Is the correct way to set the parameters to take the predicted mean given the lm, and the sd of the entire distribution of y such that:

my_object <- data.frame(x = 100)
sd <- sd(df$y)
Ey <- predict(model, new = my_object, se.fit = TRUE)$fit

gives: sd = 1.786943 Ey = 18.71

so if I now want to take multiple samples of y given x = 100 I can do

rnorm(1, Ey, sd)

taking the sd of the whole sample doesn't smell right but I can't think of any other way that you'd do it (if it is at all even possible)

[p.s. might be better suited to stackoverflow, but I assumed its more of a stats question]

Robert Hickman
  • 95
  • 5
  • 1
    @Minus Your comments might confuse the issue more than clarify it because the notation makes no distinction between the true (but unknown) parameter values and their estimates. Robert: the intuition behind the issue you bring up (as well as a correct answer) is presented in my post at https://stats.stackexchange.com/a/71303/919. – whuber Feb 26 '19 at 13:43
  • 1
    ok- will probably have to wait until later to work my way through that answer to properly understand it, but from what I gather I want to take the sd of just the residuals around the lm? (i.e. in R sd(model$residuals) ) thanks for the further reading both! – Robert Hickman Feb 26 '19 at 13:53
  • Robert Yes, that's correct: the objective of the regression is to estimate these conditional distributions. The regression equation provides the formula for their (conditional) means and--because the usual assumption is that they all have a common variance--you may estimate that common variance by combining *all* the residuals. (In more general circumstances you might look only at the residuals for values of $x$ close to $100.$) The only subtlety concerns how best to estimate the variance of all the residuals. Check out the formulas for Ordinary Least Squares regression. – whuber Feb 26 '19 at 14:02
  • 1
    Your picture of the Gaussian pdf (in red) is wrong. The x-axis should be vertical, not perpendicular to the regression line. – Stéphane Laurent Feb 26 '19 at 14:03

0 Answers0