Find a general normal stationary process

Question

I am wondering how to find the general normal stationary process satisfying $X_{n+2} + X_{n} = 0$. Any help would be much appreciated, although I am relatively new to this space so some details how to do this in general would be very nice. Alternatively please feel free to point out relevant literature online.

Answer 1

My answer is somewhat different from the one posted by @mpiktas.

Consider a discrete-time random process $X_0, X_1, X_2, \ldots$ with the property that $X_{n+2} = -X_n$. This process actually has only two random variables $X_0$ and $X_1$: everything else is predetermined since the process must necessarily be $$X_0, X_1, -X_0, -X_1, X_0, X_1, -X_0, -X_1, \cdots $$

Can such a process be a stationary process? Well, in order for the process to be stationary, it is necessary that all the random variables have the same distribution. Thus, $X_0$ and $X_1$ must have the same distribution. So must $X_0$ and $X_2 = -X_0$ have the same distribution. If $f(x)$ denotes the common probability density function of $X_0$ and $X_1$ (including as a special case a discrete density function), then $f(x)$ must be an even function of $x$. If the density function admits a mean, the mean must be $0$.
(Note that we could have $X_0$ and $X_1$ be standard Cauchy random variables whose density function is even but the mean does not exist, see e.g. the answers to this question).

Next, suppose that $(X_0,X_1)$ have joint density $f(x,y)$. If the process is stationary, then $(X_1,X_2) = (X_1,-X_0)$, $(X_2,X_3) = (-X_0,-X_1)$ and $(X_3,X_4) = (-X_1,X_0)$ all must have the same joint density. It follows that $$f(x,y) = f(y,-x) = f(-x,-y) = f(-y,x).$$ Note that this condition is always satisfied if $X_0$ and $X_1$ are independent (in addition to being identically distributed random variables with even density functions) e.g. the independent uniform $\{+1,-1\}$ random variables in @cardinal's comment on mpiktas's answer or independent zero-mean Gaussian random variables with the same variance. But I am not sure that independence is necessary for this relation to hold. (Note added in edit: In fact, as cardinal's insightful comment on this answer shows, $(X_0,X_1)$ taking on values $(1,0), (0,1), (-1,0), (0,-1)$ with equal probability satisfy the above condition but are not independent ). To tie this in with mpiktas's answer, note that if $X_0$ and $X_1$ have finite variance $\sigma^2$, then, for a stationary process, the autocorrelation function $R_X(m,m+n) = E[X_mX_{m+n}]$ (which is the same as the autocovariance function $C_X(m,m+n) = \text{cov}(X_m, X_{m+n})$ since the mean is $0$) must not depend at all on the choice of $m$, but must be a function only of $n$, the separation between the variables. From this we get that $$\text{cov}(X_0, X_1) = \text{cov}(X_1,X_2) = \text{cov}(X_1, - X_0) = -\text{cov}(X_0, X_1),$$ that is, $X_0$ and $X_1$, the only two random variables in the process, must be uncorrelated random variables. Note also that the covariance matrix in mpiktas's answer must be of the form $$\begin{bmatrix} r(0) & 0 & -r(0) & 0 & r(0) & \ldots \\ 0 & r(0) & 0 & -r(0) & 0 & \ldots \\ -r(0) & 0 & r(0) & 0 & -r(0) & \ldots \\ 0 & -r(0) & 0 & r(0) & 0 & \ldots \\ r(0) & 0 & -r(0) & 0 & r(0) & \ldots \\ \ldots & \ldots & \ldots & \ldots & \ldots \end{bmatrix}$$ In particular, there is no need to consider values of $r(1)$ other than $0$ and simulate anything to see if the eigenvalues are positive or not.

---

In summary, there do exist discrete-time stationary normal random processes with the property that $X_{n+2} = -X_n$. Such random processes are necessarily of the form $$X_0, X_1, -X_0, -X_1, X_0, X_1, -X_0, -X_1, \cdots $$ where $X_0$ and $X_1$ are zero-mean uncorrelated Gaussian random variables with the same variance. As a special case, $X_0$ and $X_1$ being independent $N(0,\sigma^2)$ random variables will work since independent Gaussian random variables are uncorrelated. But we could also have $X_1 = ZX_0$ where $Z$, which takes on values $+1$ and $-1$ with equal probability $\frac{1}{2}$, is independent of $X_0$. (This is a standard example of uncorrelated marginally Gaussian random variables that are not independent; they are not jointly Gaussian). It must also be said that these random processes are not particularly interesting as a model for random phenomena since every realization (or sample path) of the process is necessarily of the form $$a, b, -a, -b, a, b, -a, -b, \cdots$$ for independent $X_0$ and $X_1$ and of the form $$a, a, -a, -a, a, a, -a, -a \cdots~~~~~ \text{or}~~~~~ a, -a, -a, a, a, -a, -a, a,\cdots$$ for uncorrelated but not independent $X_0$ and $X_1$.

Answer 2

If the equation has a stationary solution, it is always a good idea to check whether the covariance function satisfies the required properties.

So if we assume that there is a stationary solution to an equation $X_{n+2}+X_{n}=0$, then clearly $EX_n=0$. The covariance function for such process must satisfy the following relationships

$$r(2k)=-(1)^kr(0)$$ $$r(2k+1)=-(1)^{k}r(1)$$

for all $k\in \mathbb{Z}$. But for $r$ to be a covariance function, the matrix

$$\begin{bmatrix} r(0) & r(1) & ... & r(n)\\ r(1) & r(0) & ... & r(n-1)\\ ... & ... & ... & ...\\ r(n) & r(n-1) & ... & r(0) \end{bmatrix}$$

must be semi-positive definite for each $n$. Or alternatively the inequality

$$\sum_{i=1}^n\sum_{j=1}^na_{i}a_{j}r(i-j)\ge 0$$

must hold for any $n\in \mathbb{N}$, and any $\{a_1,...,a_n\}\subset \mathbb{R}^n$.

To get an idea we can see what happens in the case $n=3$. Let us restrict $r(0)=1$, then $r(1)$ can range from $-1$ to 1, since for covariance function we must have $|r(i)|\le r(0)$ for all $i$. Now create the corresponding covariance matrix and calculate its minimal eigen value. If matrix is semi-positive definite the minimal eigen value should be non-negative. Here is the code:

> fun<-function(a,b)matrix(c(a,b,-a,b,a,b,-a,b,a),ncol=3)
> fun(1,0.4)
     [,1] [,2] [,3]
[1,]  1.0  0.4 -1.0
[2,]  0.4  1.0  0.4
[3,] -1.0  0.4  1.0

 plot(r1<-seq(-1,1,by=0.01),sapply(r1,function(x)min(eigen(fun(1,x))$values)))

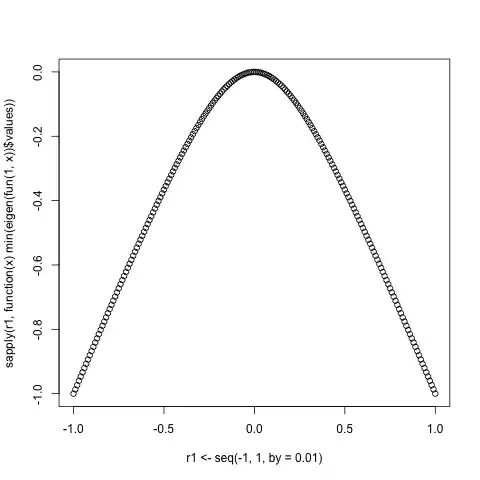
We see that minimal eigenvalues of covariance matrix is non-negative only when $r(1)=0$. For this case we have

\begin{align} \sum_{i=1}^n\sum_{j=1}^na_ia_jr(i-j)&=r(0)\sum_{k}\sum_l a_{2k}a_{2l}(-1)^{k-l}+r(0)\sum_{k}\sum_{l}a_{2k-1}a_{2l-1}(-1)^{k-l}\\ &=r(0)\left(\sum_k a_{2k}(-1)^{k+1}\right)^2+r(0)\left(\sum_k a_{2k-1}(-1)^{k+1}\right)^2\ge 0 \end{align}

So the solution exists when $r(1)=0$. Probably it is possible to prove that this is the only case, i.e. $r(1)$ cannot get any other value.