Discrete latent variables in Bayesian Network

Question

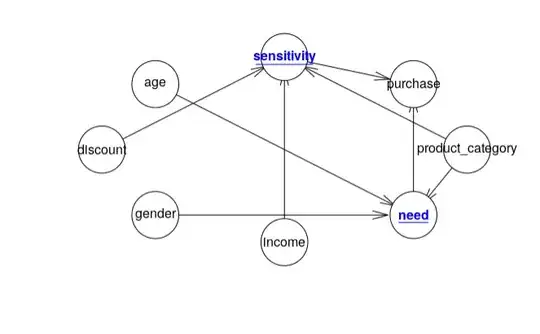
I am creating a Bayesian Network where all nodes are discrete. Using the available data, I have learned the structure of the network using the Hill-Climb algorithm (hc() function in bnlearn package in R).

Now, I wanted to introduce two discrete latent variables in the network. Since they were latent variables, I didn't have any data for them. Using intuition I incorporated the two latents into the network structure.

Take a look at the diagram for reference:

library(bnlearn)
network <- model2network("[age][gender][income][product_category][discount][need|age:gender:product_category][sensitivity|product_category:income:discount][purchase|need:sensitivity]")
plot(network, highlight=c("need", "sensitivity"), color="blue")

The goal is to predict the value of the variable purchase, which is conditionally dependent on the sensitivity and need in the given model.

I want to figure out:

• How to decide the number of classes for the discrete latent variables? Currently, I have arbitrarily set 2 classes (Yes, No) for need and 3 classes (High, Medium, Low) for sensitivity. Is there a way to get the most appropriate/optimal number of classes for the latents given data for all the other nodes?
• How to interpret the meaning of the classes of latent variables? After deciding the number and names for the classes. I ran the Expectation Maximization algorithm to get the conditional probability tables for the two latents. How do I know whether Yes and No classes (factors in R) of need mean that the need to purchase is present or not respectively?

Thanks!