I will start with the second part of your question, which pertains to the difference between randomized control studies and observational studies, and will wrap it up with the part of your question pertaining to "true model" vs. "structural causal model".
I will use one of Pearl's examples, which is an easy one to grasp. You notice that when the ice cream sales are highest (in the summer), the crime rate is highest (in the summer), and when the ice cream sales are lowest (in the winter), the crime rate is lowest. This makes you wonder whether the level of ice cream sales is CAUSING the level of crime.
If you could perform a randomized control experiment, you would take many days, suppose 100 days, and on each of these days randomly assign the level of sales of ice cream. Key to this randomization, given the causal structure depicted in the graph below, is that the assignment of the level of ice cream sales is independent of the level of temperature. If such a hypothetical experiment could be performed you should find that on the days when the sales were randomly assigned to be high, the average crime rate is not statistically different than on days when the sales were assigned to be low. If you had your hands on such data, you'd be all set. Most of us, however, have to work with observational data, where randomization did not do the magic it did in the above example. Crucially, in observational data, we do not know whether the level of Ice Cream Sales was determined independently of Temperature or whether it depends on temperature. As a result, we'd have to somehow untangle the causal effect from the merely correlative.
Pearl's claim is that statistics doesn't have a way of representing E[Y|We Set X to equal a particular value], as opposed to E[Y|Conditioning on the values of X as given by the joint distribution of X and Y]. This is why he uses the notation E[Y|do(X=x)] to refer to the expectation of Y, when we intervene on X and set its value equal to x, as opposed to E[Y|X=x], which refers to conditioning on the value of X, and taking it as given.
What exactly does it mean to intervene on variable X or to set X equal to a particular value? And how is it different than conditioning on the value of X?
Intervention is best explained with the graph below, in which Temperature has a causal effect on both Ice Cream Sales and Crime Rate, and Ice Cream Sales has a causal effect on Crime Rate, and the U variables stand for unmeasured factors that affect the variables but we do not care to model these factors. Our interest is in the causal effect of Ice Cream Sales on Crime Rate and suppose that our causal depiction is accurate and complete. See the graph below.
Now suppose that we could set the level of ice cream sales very high and observe whether that would be translated into higher crime rates. To do so we would intervene on Ice Cream Sales, meaning that we do not allow Ice Cream Sales to naturally respond to Temperature, in fact this amounts to us performing what Pearl calls "surgery" on the graph by removing all the edges directed into that variable. In our case, since we're intervening on Ice Cream Sales, we would remove the edge from Temperature to Ice Cream sales, as depicted below. We set the level of Ice Cream Sales to whatever we want, rather than allow it be determined by Temperature. Then imagine that we performed two such experiments, one in which we intervened and set the level of ice cream sales very high and one in which we intervened and set the level of ice cream sales very low, and then observe how Crime Rate responds in each case. Then we'll start to get a sense of whether there is a causal effect between Ice Cream Sales and Crime Rate or not.
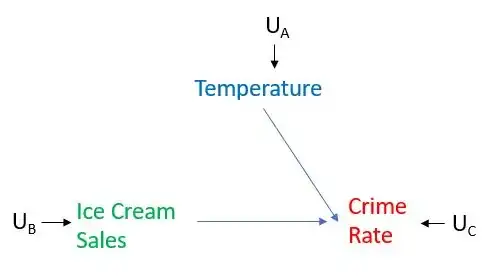
Pearl distinguished between intervention and conditioning. Conditioning here refers merely to a filtering of a dataset. Think of conditioning on Temperature as looking in our observational dataset only at cases when the Temperature was the same. Conditioning does not always give us the causal effect we're looking for (it doesn't give us the causal effect most of the time). It happens that conditioning would give us the causal effect in the simplistic picture drawn above, but we can easily modify the graph to illustrate an example when conditioning on Temperature would not give us the causal effect, whereas intervening on Ice Cream Sales would. Imagine that there is another variable which causes Ice Cream Sales, call it Variable X. In the graph is would be represented with an arrow into Ice Cream Sales. In that case, conditioning on Temperature would not give us the causal effect of Ice Cream Sales on Crime Rate because it would leave untouched the path: Variable X -> Ice Cream Sales -> Crime Rate. In contrast, intervening on Ice Cream Sales would, by definition, mean that we remove all arrows into Ice Cream, and that would give us the causal effect of Ice Cream Sales on Crime Rate.
I will just mention that one Pearl's greatest contributions, in my opinion, is the concept of colliders and how conditioning on colliders will cause independent variables to be likely dependent.
Pearl would call a model with causal coefficients (direct effect) as given by E[Y|do(X=x)] the structural causal model. And regressions in which the coefficients are given by E[Y|X] is what he says authors mistakenly call "true model", mistakenly that is, when they are looking to estimate the causal effect of X on Y and not merely to forecast Y.
So, what's the link between the structural models and what we can do empirically? Suppose you wanted to understand the causal effect of variable A on variable B. Pearl suggests 2 ways to do so: Backdoor criterion and Front-door criterion. I will expand on the former.
Backdoor Criterion: First, you need to correctly map out all the causes of each variable and using the Backdoor criterion identify the set of variables that you'd need to condition on (and just as importantly the set of variables you need to make sure you do not condition on - i.e. colliders) in order to isolate the causal effect of A on B. As Pearl points out, this is testable. You can test whether or not you've correctly mapped out the causal model. In practice, this is easier said than done and in my opinion the biggest challenge with Pearl's Backdoor criterion. Second, run the regression, as usual. Now you know what to condition on. The coefficients you'll get would be the direct effects, as mapped out in your causal map. Note that this approach is fundamentally different from the traditional approach used in estimating causality in econometrics - Instrumental Variable regressions.

