Suppose I have iid data generated from a discrete random variable $X_i \sim D(\lambda)$, and I would like to infer the parameter $\lambda$. Unfortunately, I do not know the likelihood function for $D$, but I know the generating function $G(s) = \mathbb{E}[s^X]$.
What would be the best way to do inference on this problem? I know I could get the likelihood function by taking derivatives, but this is quite cumbersome for the problem I'd like to run this on. Instead, I was thinking of calculating the observed generating function
$$ Z(s) = \frac{1}{n}\sum_i s^{X_i}$$
and numerically estimate $\lambda$.
A toy example (using Poisson) seems to work just fine:
set.seed(13)
s <- seq(0, .999, .001)
data <-tabulate(rpois(10000, 1)+1); data <- data/sum(data)
mle <- sum(data * (1:length(data)-1))
o <- outer(s, 0:(length(data)-1), function(x,y)x^y)
x <- colSums(data * t(o))
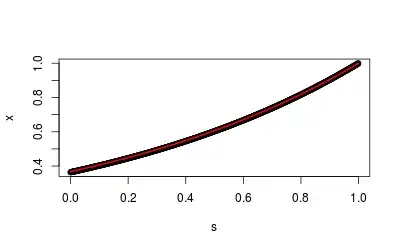
plot(s, x, main="empirical vs expected GF" )
lines(s, exp(s-1), col=2, lwd=2)
lambda.hat <- optim(par=1,
function(lambda)sum((x - exp(lambda *(s-1)))^2),
lower=.1, method="L-BFGS-B", upper=10)
The GF-based estimate is very similar to the MLE, so this seems to work in practice:
> lambda.hat$par
[1] 1.011152
> mle
[1] 1.0129
Thus my questions are: Does this type of inference scheme have a name/literature? Are there any guidelines when it would be appropriate to use? Are there any caveats to keep in mind?