2

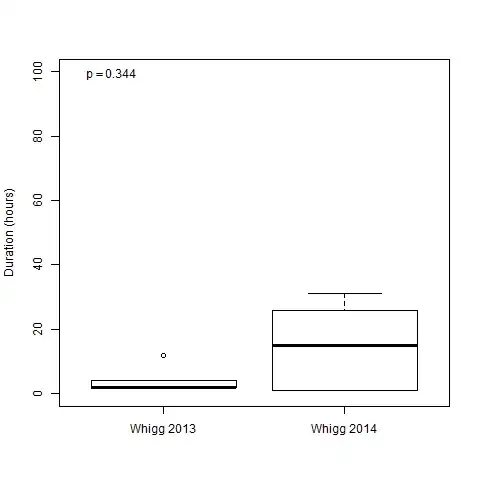
I am comparing two sets of data using the Wilcoxon Rank Sum test. Although the distributions appear to be quite different, the p-value is quite high (0.344).

This is the line of code being used for the test:

WG2013_data$Duration <- c(2, 2, 4, 4, 12, 2, 2)
WG2014_data$Duration <- c(1, 26, 1, 31, 18, 12)
wcx <- tidy(wilcox.test(WG2013_data$Duration, WG2014_data$Duration))

enter image description here

There are 7 samples in the WG2013_dataand 6 samples in the WB2014_data. Could it be that the unequal sample sizes is causing the high p-value?

Should I set any options as TRUE/FALSE?

I've also tried the Kolmogorov-Smirnov test:

ks <- tidy(ks.test(WG2013_data$Duration, WG2014_data$Duration))

And the Kruskal–Wallis test:

kruskal <- tidy(kruskal.test(Duration ~ Year, data = WG_data))

Both of these tests also show p-values of about 0.34.

Welch's t-test gives a p-value = 0.089, so this at least shows a significant difference in the mean at p < 0.1, but the Whigg 2013 data are not normal according to a qqplot and Shapiro-Wilk test.

Is there another non-parametric test I should try?

viridius
  • 41
  • 1
  • 1
  • 3
  • also: http://www.real-statistics.com/non-parametric-tests/wilcoxon-rank-sum-test/ (illustrates how Wilcoxon works for unequal sample sizes) – Ben Bolker Sep 25 '18 at 22:47
  • 1
    Thanks @BenBolker. Apologies for not getting this onto CrossValidate in the first place. I am not trying to 'hack' for a significant p-value. I'm just trying to be sure that I am applying the test correctly since the high p-values on the non-parametric test were unexpected. – viridius Sep 25 '18 at 22:51
  • since it has no answers as yet, you could choose to delete and re-post on CV yourself - or you could wait for it to be migrated. (I think it would be a bit rude to delete/re-post once someone has already put effort into an answer ...) – Ben Bolker Sep 25 '18 at 22:52
  • 1
    By the way, it might be useful to post the data - since there are only 13 values, it shouldn't be too overwhelming ... – Ben Bolker Sep 25 '18 at 22:53
  • 1
    post your real data – Edward Sep 25 '18 at 23:03
  • Data has been posted – viridius Sep 25 '18 at 23:09
  • Your samples differ only by 1 unit, so this really shouldn't affect p-values. – user2974951 Sep 26 '18 at 06:46
  • Somewhat of an ambiguous comment @user2974951. Perhaps you are meaning that since the four lowest values in `WG2013_data` are higher (albeit only slightly) than the two lowest values in `WG2014_data`, the ranked basis of the Wilcoxon Rank Sum test is sufficient to determine the "two distributions are not significantly different" (in quotes since I realize this is not the precise hypothesis being tested). Is there some sort of hybrid between Welch's t-test and the Wilcoxon Rank Sum test? (moderators, please migrate this post to CrossValidated, if possible) – viridius Sep 26 '18 at 15:44

2 Answers2

2

The Wilcoxon Rank Sum test (aka Mann-Whitney) works with unequal sample sizes.

The original paper (referenced below) did some analyses with different sample sizes and showed its consistency and asymptotic normality (see table I, n = 8 on page 54). They also go on to show its robustness for small sample sizes.

Reference: Mann, Henry B.; Whitney, Donald R. (1947). "On a Test of Whether one of Two Random Variables is Stochastically Larger than the Other". Annals of Mathematical Statistics 18 (1): 50–60.

daszlosek
  • 121
  • 8
1

Boxplots are a bad choice to display small data sets. Try a plot like this with one point per data point for better intuition:

Duration1 <- c(2, 2, 4, 4, 12, 2, 2)
Duration2 <- c(1, 26, 1, 31, 18, 12)

plot(x=Duration2, y=jitter(rep(.2, length(Duration2)), 2), ylim=c(0,1), yaxt="n", pch=1)
points(x=Duration1, y=jitter(rep(.8, length(Duration1)), 2), pch=2)
axis(2, at=c(.2, .8), labels=c("dur2", "dur1"))

enter image description here

Now consider, that the test can only see ranks. The smallest value and the three largest values belong to duration 2, the two with value 12 do not add to a difference. It will then become more intuitively valid that the order of the circles and triangles is not very convincing, i. e. $p$ should be large.

In a comment you asked:

Is there some sort of hybrid between Welch's t-test and the Wilcoxon Rank Sum test?

There is no description of what the hybrid is supposed to do. Comparing means with no normality assumptions? You could try bootstrapping or permutation tests.

Duration1 <- c(2, 2, 4, 4, 12, 2, 2)
Duration2 <- c(1, 26, 1, 31, 18, 12)

true.diff <- mean(Duration1) - mean(Duration2)
bootstrapped.diffs <-replicate(10000, mean(Duration1[sample(1:7, replace=TRUE)])-mean(Duration2[sample(1:6, replace=TRUE)]))

hist(bootstrapped.diffs, breaks = 30)
abline(v = true.diff, col = "red", lwd = 3)
sum(bootstrapped.diffs > 0)/10000
Bernhard
  • 7,419
  • 14
  • 36