Visualising plausible values in multiple imputation

Question

I have been checking density plots to get a feel for the plausibility of values that have been imputed using the mice package in R. I would be grateful for some advice/guidance/comment on the following problem. The imputations are created by a call to mice() :

require(mice)
imp <- mice(...) 

The details omitted as it a lot of code and a large dataset. Hopefully this won't detract from the question. This is the plot which is generated by the built-in densityplot function in the mice package: densityplot( x=imp , data= ~ age)

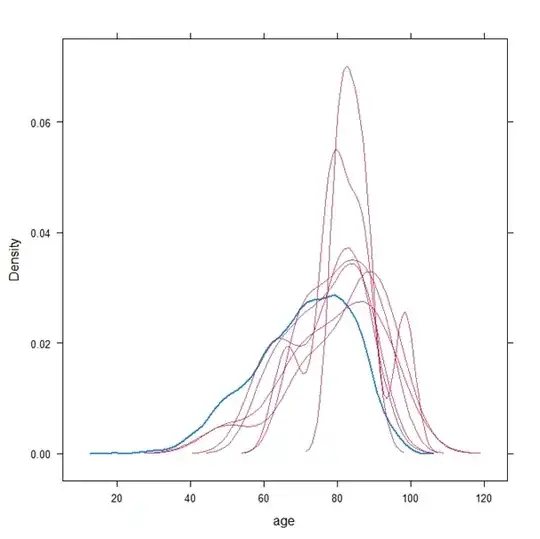
The blue line is the observed data, the red lines are the imputed data. This caused me some alarm. Particularly:

1. Since the observed data are fully contained in each imputed dataset, how can some values which appear in the observed data have a zero density in the imputed data ?

2. There are 7019 observations of which only 11 are missing, so I would expect the imputed densities to be nearly identical to the observed.

3. In a general sense, how can the plots look so different ?

So I compared it to a plot using ggplot:

require(ggplot2)
require(reshape)

fortify.mids <- function(x){
 imps <- do.call(rbind, lapply(seq_len(x$m), function(i){
   data.frame(complete(x, i), Imputation = i, Imputed = "Imputed")
 }))
 orig <- cbind(x$data, Imputation = NA, Imputed = "Observed")
 rbind(imps, orig)
}

x11()
ggplot(fortify.mids(imp), aes(x = age, colour = Imputed, 
   group = Imputation)) +
geom_density() + 
scale_colour_manual(values = c(Imputed = "#000000", Observed = "#D55E00"))

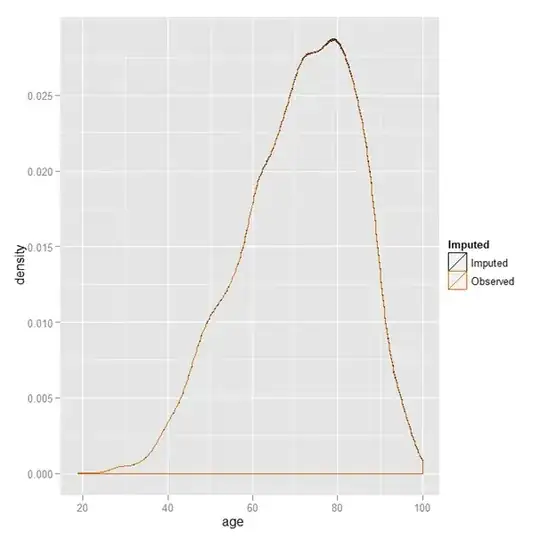
And as you see, all the densities overlap (you can't even really notice that there is more than 1 line).

Can anyone explain what is going on with the first plot ? Note that the data used to generate these 2 plots is the same.

Answer 1

(Previously I had added this as a comment).

I believe the densityplot function from mice is displaying the observed values in blue and only the 11 imputed values from each of your 7 imputations (or however many you requested) in pink. Because only 11 values are imputed in each imputation, extreme values affect the shape of these plots dramatically. Despite this, the central tendencies of the density plots of imputed data appear relatively similar -- exactly what you want. In your second plot, it looks like you've plotted both observed and imputed data in each density plot, so all the distributions overlap quite a bit.