6

If I understand it correctly, linear regression finds one best fitting line for the given data. It can do it either by using calculus and solving for intercept and slope equations or it can solve it using an optimization method such as gradient descent.

Now, I don't understand why all statistical software return a distribution of coefficients (along with estimates, standard error, t-value, confidence interval), when we only have one line and it should have one value of slope and intercept. Do the residuals have something to do with it?

Edit: It appears that my choice of words "distribution of coefficients" caused some confusions. I meant to refer to the estimated coefficient distribution given in the output as shown below:

tis confusion

sircasms
  • 63
  • 6
  • 1
    Can you clarify what you mean by all statistical software returning a "distribution of coefficients"? I've been using software to do regression regularly since the start of the 1980s (and even a few times in the 70s) across dozens of different programs and I find myself unable to figure out what you're saying all those programs do. In what form is this distribution given? (a drawing of a density or cdf? as an algebraic formula?). Can you show an example (that isn't any of the things you list under 'along with', since clearly those are meant to be in addition to the distribution you mention) – Glen_b Aug 04 '18 at 00:36
  • I feel grateful to receive a comment from you. Thank you for making this industry welcoming for newbies and popular among everyone. Please refer to the comments below for clarification. – sircasms Aug 04 '18 at 04:57
  • 1
    If you mean the answers, I read them prior to commenting but I didn't see anything in them that I could relate to what your question seemed to be suggesting and indeed they seem to be answering entirely different questions, so I doubt they can both be responding to whatever it is you're asking about (one or the other might, but perhaps neither do). Can you please clarify, in your question what you mean by a "distribution of coefficients"? If you're not sure how to describe it, could you show an example? – Glen_b Aug 04 '18 at 06:57
  • 1
    sircasms, I thought I originally understood this question, but the posted answers demonstrate that others have a rather different understanding of it. This explains why both (a) you have received different answers yet (b) the question has many upvotes: evidently users like the question, but they might be liking a set of different questions! Ambiguous situations like this are really bad, because people can easily be misled about what is being asked as well as what is being answered. @Glen was right to ask you to clarify the post. – whuber Aug 04 '18 at 12:39
  • I see the confusion. Please check the edited question. – sircasms Aug 04 '18 at 16:51
  • And, I don't believe the current two answers are conflicting or different. They shared specific opinions as to why linear regression predicted a "distribution of beta" rather than one value. – sircasms Aug 04 '18 at 16:54
  • 1
    The source of the confusion etc. is that you are using "distribution" in a non-standard way. In statistics, "distribution" refers to a probability distribution, e.g., Gamma, Pareto, ..., and, depending upon circumstances, the parameters of that distribution. This is not what is being returned in the table above. The table returns the estimated value and an estimate of how accurate it is (the std. error) at estimating the true underlying population parameter. This is not a distribution in the statistical sense of the word. – jbowman Aug 04 '18 at 17:22
  • Got it! Guess I got lucky that people in the two comments understood what I meant. – sircasms Aug 04 '18 at 17:38

2 Answers2

7

Consider the difference between a population and a sample taken from that population.

You are correct that standard linear regression provides a unique best fitting line for the given data: for this one sample from a population of cases.

We are generally, however, interested in the characteristics of the population, not just of the sample. The reported distribution of coefficient values represents how those values might change over repeated sampling from the same population.

And, yes, the residuals have much to do with one way to estimate the distribution of coefficients, as explained for example here, based on certain standard assumptions. Resampling provides another way to estimate that distribution without making those assumptions.

EdM
  • 57,766
  • 7
  • 66
  • 187
6

The true parameter/regression coefficients

Linear regression assumes the model:

$$y_i = \boldsymbol{\beta} \mathbf{x_i} +\epsilon_i$$

where $\boldsymbol\beta$ is assumed fixed and only the residual term $\epsilon_i$ is assumed to be distributed according to some distribution.

So the true parameter/coefficient is assumed fixed, and is not assumed to be related to a distribution (That is in linear regression, one could think of alternative models that do express distributions for the coefficients)

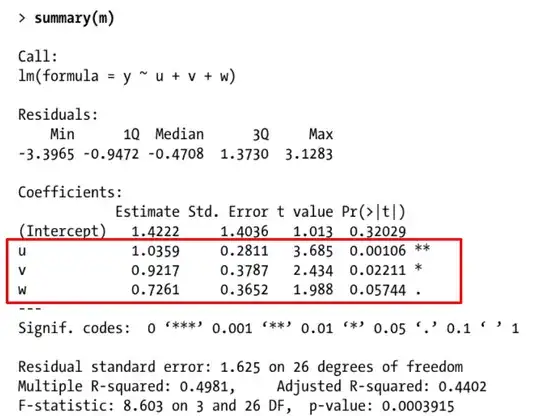
The estimated parameter/regression coefficients

While the true $\boldsymbol{\beta}$ may be fixed, the estimated $\boldsymbol{\hat\beta}$ may be considered to follow some distribution (the estimate depends on a sample/data that varies for every new experiment, thus the estimate can be considered a random variable). This leads to two different way to express the estimation of the parameter, point estimates and interval estimates, and in this difference you may find the intuition for reporting additional estimates as standard error, t-value, confidence interval:

  • From https://en.wikipedia.org/wiki/Point_estimation

    In statistics, point estimation involves the use of sample data to calculate a single value (known as a point estimate or statistic) which is to serve as a "best guess" or "best estimate" of an unknown population parameter (for example, the population mean). More formally, it is the application of a point estimator to the data to obtain a point estimate.

  • From https://en.wikipedia.org/wiki/Interval_estimation

    In statistics, interval estimation is the use of sample data to calculate an interval of plausible values of an unknown population parameter; this is in contrast to point estimation, which gives a single value. Jerzy Neyman (1937) identified interval estimation ("estimation by interval") as distinct from point estimation ("estimation by unique estimate"). In doing so, he recognized that then-recent work quoting results in the form of an estimate plus-or-minus a standard deviation indicated that interval estimation was actually the problem statisticians really had in mind.

The interval estimate gives a bit better idea about what information the data carries. It is not only an estimate for a single population parameter, but it also conveys something like the strength of the information that the data carries, ie how far other values than this single estimate, $\boldsymbol{\hat\beta}$ , could still be reasonable alternatives for the unknown parameter $\boldsymbol{\beta}$.

More data, or data with less noise, leads to a smaller deviance of the estimate $\boldsymbol{\hat\beta}$ (and this deviance can be estimated from the data), which means that not every point estimate can be considered the same. With more data or smaller noise levels the estimate is more likely 'close' to the true unknown parameter. Just a single point estimate does not convey this deviance and how 'close' the point estimate likely is.

Community
  • 1
Sextus Empiricus
  • 43,080
  • 1
  • 72
  • 161