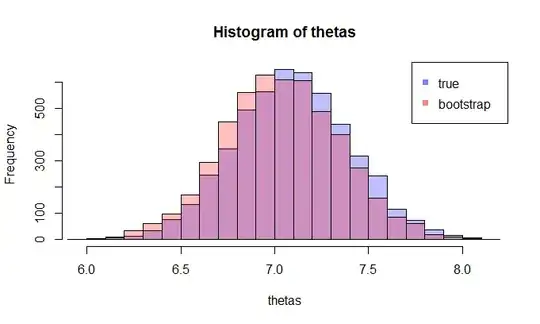
Having recently studied bootstrap, I came up with a conceptual question that still puzzles me:
You have a population, and you want to know a population attribute, i.e. $\theta=g(P)$, where I use $P$ to represent population. This $\theta$ could be population mean for example. Usually you can't get all the data from the population. So you draw a sample $X$ of size $N$ from the population. Let's assume you have i.i.d. sample for simplicity. Then you obtain your estimator $\hat{\theta}=g(X)$. You want to use $\hat{\theta}$ to make inferences about $\theta$, so you would like to know the variability of $\hat{\theta}$.
First, there is a true sampling distribution of $\hat{\theta}$. Conceptually, you could draw many samples (each of them has size $N$) from the population. Each time you will have a realization of $\hat{\theta}=g(X)$ since each time you will have a different sample. Then in the end, you will be able to recover the true distribution of $\hat{\theta}$. Ok, this at least is the conceptual benchmark for estimation of the distribution of $\hat{\theta}$. Let me restate it: the ultimate goal is to use various method to estimate or approximate the true distribution of $\hat{\theta}$.
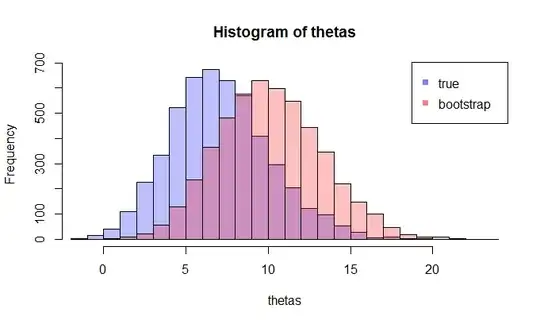
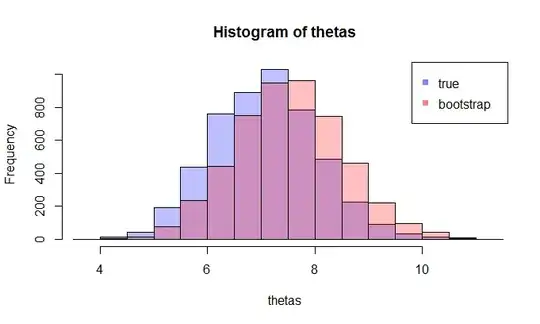
Now, here comes the question. Usually, you only have one sample $X$ that contains $N$ data points. Then you resample from this sample many times, and you will come up with a bootstrap distribution of $\hat{\theta}$. My question is: how close is this bootstrap distribution to the true sampling distribution of $\hat{\theta}$? Is there a way to quantify it?
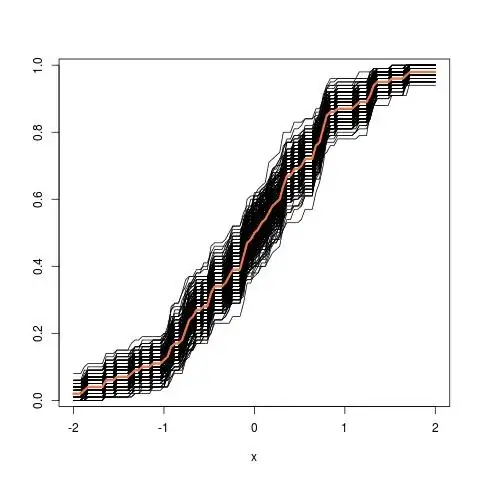
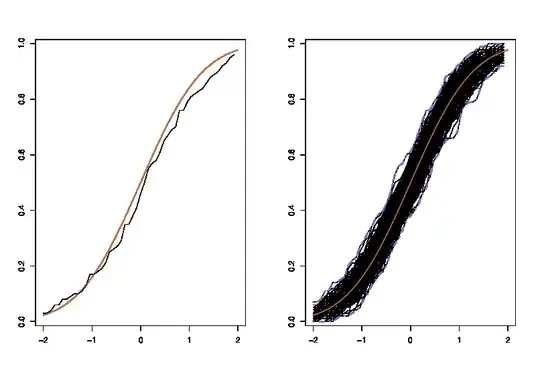 where the lhs compares the true cdf $F$ with the empirical cdf $\hat{F}_n$ for $n=100$ observations and the rhs plots $250$ replicas of the lhs, for 250 different samples, in order to measure the variability of the cdf approximation. In the example I know the truth and hence I can simulate from the truth to evaluate the variability. In a realistic situation, I do not know $F$ and hence I have to start from $\hat{F}_n$ instead to produce a similar graph.
where the lhs compares the true cdf $F$ with the empirical cdf $\hat{F}_n$ for $n=100$ observations and the rhs plots $250$ replicas of the lhs, for 250 different samples, in order to measure the variability of the cdf approximation. In the example I know the truth and hence I can simulate from the truth to evaluate the variability. In a realistic situation, I do not know $F$ and hence I have to start from $\hat{F}_n$ instead to produce a similar graph.