3

Multiple imputation is known to be advantageous compared to single imputation. However, in practice there are often non-statistical reasons why multiple imputation can not be used (e.g. the data recipient isn't educated enough to deal with multiple data sets; the boss of a company doesn't want it; ...).

Predictive mean matching (PMM) is a bayesian imputation method that is known to be one of the best imputation methods, when multiple imputation can be applied. Now, I am wondering whether PMM could also be used as single imputation method, when multiple imputation is not possible.

Consider the following example:

  • You have a typical data set including a continous variable (e.g. income / age) with missing values.
  • The data can be imputed only once (single imputation).
  • You have to choose between typical single imputation methods (e.g. stochastic regression imputation / hot deck imputation) OR predictive mean matching.

Illustration in R:

# Create some example data
set.seed(95159)                      # Seed
N <- 20000                           # Sample size

y <- rnorm(N)                        # Target variable
x1 <- rnorm(N) + 0.1 * y             # Some auxiliary variables
x2 <- rnorm(N) - 0.05 * y
x3 <- rnorm(N) + 0.2 * x1 + 0.3 * x2

y[rbinom(N, 1, 0.1) == 1] <- NA      # 10% missings in y

data <- data.frame(y, x1, x2, x3)    # Create data set


# Impute data via stochastic regression imputation
# and predictive mean matching
library("mice")                      # Load mice package

imp_sri <- mice(data, m = 1, method = "norm.nob")
imp_pmm <- mice(data, m = 1, method = "pmm")

data_sri <- complete(imp_sri)
data_pmm <- complete(imp_pmm)


# Compare results
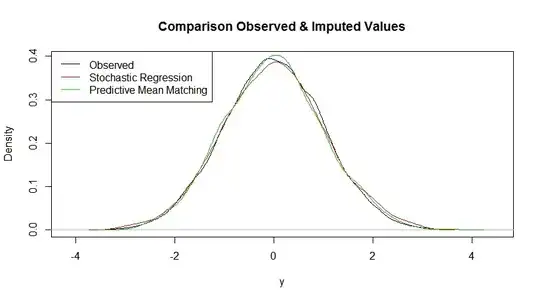
plot(density(data$y, na.rm = TRUE), xlab = "y",
     main = "Comparison Observed & Imputed)

points(density(data_sri$y[is.na(data$y)]), typ = "l", col = 2)
points(density(data_pmm$y[is.na(data$y)]), typ = "l", col = 3)

legend("topleft",
       c("Observed", "Stochastic Regression", "Predictive Mean Matching"),
       col = c("black", "red", "green"), lty = 1)

enter image description here

The simplified example doesn't reveal a substantial difference between stochastic regression imputation and single predictive mean matching. However, in more complex data scenarios (e.g. heteroscedastic data), predictive mean matching is usually advantageous.

Question: If multiple imputation can not be used, is there any reason, why single predictive mean matching should not be used instead of typical single imputation methods such as stochastic regression imputation?

Frank Harrell
  • 74,029
  • 5
  • 148
  • 322
Joachim Schork
  • 1,068
  • 4
  • 15
  • 37

1 Answers1

3

The two approaches should be equally good or bad. The bigger point is that a boss who wants you do dumb down an analysis is not respecting the statistician for her area of expertise. Single imputation, whether regression or PMM can be used as you did by taking only one draw, and the resulting fitted equation will be nearly unbiased. But it will have higher variance and we'll have no way of getting standard errors on the coefficient estimates. So inform your boss of what exactly the trade-offs are.

Frank Harrell
  • 74,029
  • 5
  • 148
  • 322
  • Thank you very much for your response! I am fully aware that single imputation has disadvantages and I explained this many times (without success). However, good to get confirmed that predictive mean matching has no "hidden" drawbacks, since I think predictive mean matching has many advantageous compared to other methods (e.g. better handling of heteroscedastic data or no imputation of implausible values). – Joachim Schork Aug 06 '18 at 12:30
  • Just remember that if single imputation is meant to imply single conditional mean imputation, then there are real problems in the final model. Conditional mean imputation is not stochastic enough. – Frank Harrell Aug 06 '18 at 18:18
  • Thanks for the hint. I'm planning to use predictive mean matching as illustrated in the R code of my post above. – Joachim Schork Aug 07 '18 at 07:20
  • 2
    There is one hidden drawback of PMM. If you have mechanistic missing, the imputed values will just hit a boundary and will be biased. For example if everyone with x > 10 has missing z, imputations for z will be near what you would get for x=10 but not properly extrapolate. Regression imputation, though assuming an unverifiable model for this situation, will extrapolate as it should. – Frank Harrell Aug 12 '18 at 11:43
  • Thanks a lot for getting back to me on that. Good point, I haven't thought about that yet. However, I think in my specific situation it is relatively safe to assume that the data set is not affected by this problem. – Joachim Schork Aug 13 '18 at 08:26