Why is odds ratio an estimate of relative risk?

Question

This link says

In epidemiological terms, the odds ratio is used as a point estimate of the relative risk in retrospective studies.

I understand that odds ratio is calculated in case control studies, while relative risk is calculated in cohort studies. Calculating incidences and risks in case control studies doesn't make sense because we ourselves are choosing the ratio of cases and controls which is never how it happens in nature. But it is usually taught that, odds ratio gives an estimate of this.

Why is this so?

Answer 1

It is not true in all situations. The odds ratio only gives an estimate of the relative risk if the outcome is a low probability outcome. (Same insight as Poisson approximation to the binomial distribution).

Imagine a case-control study for lung cancer, then we check the number of smokers in both groups. Technically, the only thing we can test is given that an individual has lung cancer, what is the probability that they smoke. We can do the same for the non cancer group, and obtain a ratio of the both probabilities. This would be the relative risk. But we do not really care about this quantity. We actually want, given that an individual smokes, what is the probability that they have lung cancer divided by the same probability for non-smokers.

The nice thing about the odds ratio is that it is bi-directional. So: the odds of smoking given lung cancer divided by the odds of smoking given control is actually equivalent to the odds of lung cancer given smoking divided by the odds of lung cancer without smoking. This bi-directionality of the odds ratio allows us to obtain the comparison we want from case-control studies.

Now, if we know the outcome to have a low rate in both groups $-$ the proportion of individuals with lung cancer is small among smokers and non-smokers $-$ then the odds ratio approximates the relative risk. This is the one time we can use the odds ratio to approximate the relative risk in case-control studies. I'm assuming that in case-control studies, the cases are rare events. So certain persons may skip this caveat and state what the OP stated.

The best resource I've found for questions like the one here is Agresti's book on Categorical Data Analysis.

Answer 2

The quote surely just means to say that the odds ratio is a relative risk measure - rather than an estimate of the relative risk, which as already point out is only approximately the case in cohort studies/randomized trials for very low proportions.

By relative risk measure I mean something that is given relative to some comparison group in a way that the absolute difference depends on the value for the comparison group.

I.e. if the odds ratio is 2, then if the odds of an event are 1:1 (50% probability) in the control group, they are 2:1 (67% probability) in the test group for a 17% absolute risk difference, but for control group odds of 1:99 (1%), it is a 2:99 (2%) test group odds for a 1% absolute risk difference. The relative risk has a similar property - except that it cannot remain constant across all control group probabilities, a relative risk of 2 is only possible for a control group probability $\leq 50\%$ - and so do the hazard ratio, as well as the rate ratio. I believe these four measures of usually meant when people talk about measures of relative risk. It is of course confusing that one of them is called "relative risk".

Answer 3

This was an interesting question so I did a little digging. The first link I found gave a little bit of insight.

The basic difference is that the odds ratio is a ratio of two odds (yep, it’s that obvious) whereas the relative risk is a ratio of two probabilities (the relative risk is also called the risk ratio).

The odds ratio is the ratio of the odds of an event in the Treatment group to the odds of an event in the control group. The term ‘Odds’ is commonplace, but not always clear, and often used inappropriately. The odds of an event is the number of events / the number of non-events.

The article also gave the following equations, which make the difference a bit easier to understand:

Suppose you have a school that wants to test out a new tutoring program. At the start of the school year they impose the new tutoring program (treatment) for a group of students randomly selected from those who are failing at least 1 subject at the end of the 1st quarter. The remaining students receive the customary academic support (control group).

At the end of the school year the number of students in each group who fail any of their classes is measured. Failing a class is considered the outcome event we’re interested in measuring. From these data we can construct a table that describes the frequency of two possible outcomes for each of the two groups.

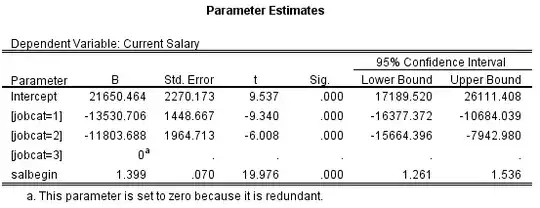
Based on the definition from this site, OR and RR are two fundamentally different concepts.

$$ OR = \frac{a d}{b c} \\ RR = \frac{\frac{a}{a+b}}{\frac{c}{c+d} } = \frac{a \cdot (c+d)}{c \cdot (a+b)} = \frac{ac + ad}{ca + cb} $$

This may not be particularly helpful yet, but I found another article that was more insightful. It was aptly named Relative risks and odds ratios: What’s the difference?, and explains the ratios in the following way...

Probability is the likelihood of an event in relation to all possible events. If a horse wins 2 out of every 5 races, its probability of winning is 2/5 (40%). Relative risk is a ratio of probabilities. It compares the incidence or risk of an event among those with a specific exposure with those who were not exposed (eg, myocardial infarctions in those who smoke cigarettes compared with those who do not). RR is based upon the incidence of an event given that we already know the study participants’ exposure status. It is only appropriate, therefore, to use RR for prospective cohort studies.

Odds compare events with nonevents. If a horse wins 2 out of every 5 races, its odds of winning are 2 to 3 (expressed as 2:3). An odds ratio is a ratio of ratios. It compares the presence to absence of an exposure given that we already know about a specific outcome (eg, presence-to-absence ratio of cigarette smoking in those who had an MI compared with the same ratio in those who did not have an MI). OR can be used to describe the results of case control as well as prospective cohort studies.

OR and RR are usually comparable in magnitude when the disease studied is rare (eg, most cancers). However, an OR can overestimate and magnify risk, especially when the disease is more common (eg, hypertension) and should be avoided in such cases if RR can be used.

From this article, we can see that one would be able to reasonably estimate relative risk with the odds ratio if the disease is rare. This addresses the "the odds ratio is used as a point estimate of the relative risk in retrospective studies" quote in your original question. Though we are not provided with the original source of your quote, one could assume you pulled the quote from a source relating to relatively rare diseases, or disease outbreaks.

As a caveat, note the following information from this document, which also examines these two terms:

The RR and the OR should always be examined in the context of the absolute risk. For example, in a case-control study, Louik at al. found that the use of sertraline during pregnancy substantially increased the risk for omphalocele (OR=5.7; 95% CI, 1.6-20.7). Omphalocele is rare in the population, and so, in this situation, the OR and the RR would probably be similar. If the risk of omphalocele in the general population is 0.02%, the 5-fold increased risk with sertraline would result in an incidence of 0.01%. At the individual patient level, 0.1% is an almost negligible risk. Therefore, when the absolute risk is low, even a large increase in the RR or OR may not be clinically significant.

The absolute risk of an event is the likelihood of occurrence of that event in the population at risk.