I am trying to determine the distribution of my data to carry out a glmer. Indeed, I need to write the term 'family = X' in the command of the glmer but I am not able to find the distribution.
Model is of this type:
mod4<-glmer(Correct_TL~Temperature*Population + Size + (1|Measurement), data=df, family=X)
The response variable 'Correct_TL' contains negative values as it corresponds to the difference between total length of each individual and the mean of its group.
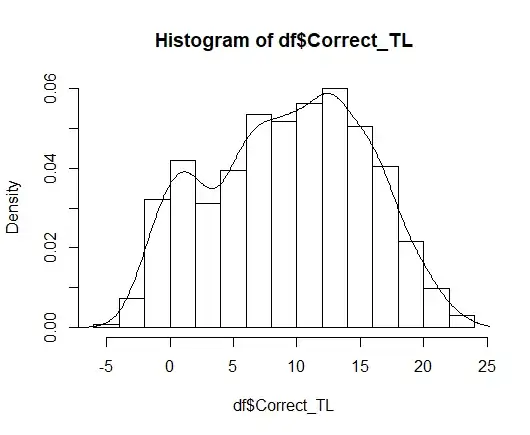
I plotted the data as follows and got this graph:
hist(df$Correct_TL, freq=FALSE)
lines(density(df$Correct_TL))
Then, I run the following command (I read some discussions):
library(fitdistrplus)
descdist(df$Correct_TL, discrete = FALSE)
normal_dist <- fitdist(df$Correct_TL, "norm")
plot(normal_dist)
And got this:
I am really not familiar with this. But looking at the graphs, I would say data could be considered as normal. What do you think ? Do you have any idea of what else it could be ? I tried to do the same for gamma and lognormal distributions but as I have negative values, it does not work.