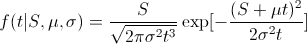How to improve forecast accuray of bsts model

Question

I have a question about the use of the bsts package. In general my question is if my approach is feasible. Because my holdout MAPE is much worse than all the other approaches I have in my ensemble.

Here is my code.

library("bsts")
library("ggplot2")
library("reshape")
# split into test and train ------------------------------------------------------
date <- as.Date("2017-06-04")
horizon <- 105
model.data$DATUM <- as.Date(model.data$DATUM)
xtrain <- model.data[model.data$DATUM <= date,]
xtest <- model.data[model.data$DATUM > date,]

# building the first model ------------------------------------------------------
ss <- list()
ss <- AddSemilocalLinearTrend(ss, xtrain$ITEMS)
ss <- AddSeasonal(ss,xtrain$ITEMS,nseasons = 52,
                  season.duration = 7)

# V7 is a dummy variable for the one outlier
fit <- bsts(ITEMS ~ V7 ,
            data = xtrain,
            seed = 100,
            state.specification = ss,
            niter = 1500)

# validation --------------------------------------------------------------------
burn <- SuggestBurn(0.1,fit)
fcast.holdout <- predict(fit,
                         newdata = xtest,
                         h = horizon,
                         burn = burn)

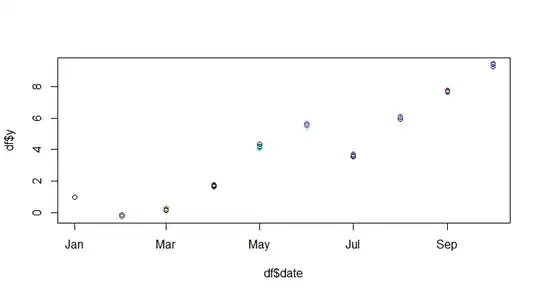
validation.time <- data.frame("semi.local.linear.bsts" = as.numeric(fcast.holdout$mean),
                              "actual" = model.data[model.data$DATUM > date,"ITEMS"],
                              "datum" = model.data[model.data$DATUM > date,"DATUM"])

a <- melt(validation.time,id.vars = c("datum"))
ggplot(data = a,
       aes(x = datum, y = value, group = variable,color = variable))+
       geom_point()+
       geom_line()

plot(fcast.holdout)

The data can be found here. The data are daily sales data for a retail shop. Later I want to include some dummy variables which you can also find in the example data.

For me the main questions are:

Is the seasonal part correctly defined? I have a annual seasonality in my data and also a weekly pattern. However in the validation plot I cannot find the weekly pattern.

Why do I have such high prediction intervals? Should I change the trend part?

what country is your data from ... AUTOBOX utilizes country-specific holiday schedules as it individually optimizes the lead and lag ( window of response ) around each holiday. Outliers often suggest the need for additional indicators which is why you don't clean them out as @alex naively suggests . This is akin to "throwing out the baby with the bathwater" . — IrishStat, Jul 24 '18 at 15:24

score 1 · Answer 1 · answered Jul 23 '18 at 17:48

1

Clean out the outlier instead of using a dummy variable (use tsclean()). Try AddTrig instead of AddSeasonal for there seasonal component, since your data seems to have multiple seasonalities.

What other methods are you using that are giving better results than BSTS?

answered Jul 23 '18 at 17:48

Skander H.

10,602
2
33
81

Unfortunately that won't quite work as some "outliers" can be seasonal in nature ... – IrishStat Jul 23 '18 at 21:39
@IrishStat then they aren't outliers. They are seasonal events that should be modeled as exogenous variables. – Skander H. Jul 23 '18 at 21:41
that is correct ... the should be identified and added . Note I put quotes around "outliers" to suggest that they weren't really outliers – IrishStat Jul 23 '18 at 21:48
Outlier was the wrong term then. This "outlier" will occur every year again. The definition of outlier is not stringent I think. So, I will still include the dummy variable. – burton030 Jul 24 '18 at 09:13
I will try the approach with the trigonometric functions for the seasonal patterns. I was not aware of this possibility in bsts. I have good experience with this procedure for modeling the seasonality in other approaches that I tried. – burton030 Jul 24 '18 at 09:18
the seasonal structure /acivity is for 6 months of the year (3,4,5,6,7 and 11) and for the first 5 days . Fitting is not modelling . – IrishStat Jul 24 '18 at 09:52
@Alex Would you suggest to define the seasonal part as the following `AddTrig(ss,xtrain$ITEMS, period = 365.25, frequencies = c(1,52))`?? – burton030 Jul 26 '18 at 15:53

IrishStat · Answer 2 · 2018-07-24T20:36:10.037

Your approach is feasible but you need to accommodate many more columns (i.e. predictor series) than you have. I took your data into a comprehensive time series package that simultaneously deals with i.e. identifies 1) lead and lag effects around holidays 2) day-of-the-week effects and changes in day-of-the-week effects 3) time trends and level shifts 4) day-of-the-month effects % 5) week=of-the-month effects , 6) month-of-the-year effects 7) week-of-the-year effects 8) long-weekend effects 9) anomalies 10) changes in error variance over time and others including user-specified/suggested causals et al and of course any necessary arima structure to deal with omitted structure.

This is the Actual/Fit and Forecast that you should be getting from a useful model with model residuals here and forecasts here for the next 365 days .

Part of the equation is shown here and here

Hope this helps raise your expectations regarding daily modelling . solutions....

If you can find a way to identify these additional "columns" for your data you possibly might be able to something useful out of your current approach. Of course the trick is this do this automatically/programattically as I did.

Your "lack of confidence in your results" is echoed/mirrored by the "lack of confidence in your forecasts i.e. unrealistically very wide prediction limits "

In help to Alex , I have added more of the equation explicitely showing the indicator series for some of the Pulses ..

I was asked to provide a clear picture of the forecasts vis-a-vis the actuals

@jan-mrozowski The comprehensive time series package is called is called AUTOBOX https://autobox.com/capable.pdf which I helped to develop. — IrishStat, Jun 03 '19 at 21:01

How to improve forecast accuray of bsts model

2 Answers2